データサイエンス入門

おまけ：ロジスティック回帰分析。

データサイエンス入門の範囲外ですが「何時間くらい練習すれば、ある技量を身に着けられるか？」とか「血糖値がいくらくらいだと糖尿病の可能性がどのくらいあるか？」とか、「連続値(独立変数=説明変数)と２値（Yes/No：従属変数：目的変数）の関係」をモデル化して、連続値からYes/No の確率を推定する方法を紹介しましょう。これは、ロジスティック回帰分析と呼ばれていますが... 例によって「名前の由来(意味)は不明」ということで名前の由来などの詳しい説明は省略しますが、まあ「名前に意味の無い固有名詞」と思ってください(^^;（ロジスティック=logistic ですが、例によって「物流」の意味ではありません(^^;）

医療系では様々な診断の目安を決めるために使われますし、ビジネスの世界なら様々な意思決定に、また、AI（ニューラルネットワーク）の１つのニューロン（神経細胞）の学習モデルとしても、使われます。今後、様々な分野での「データによる意思決定」や「ＡＩによるデータ処理」の仕組みを学ぶ上での基礎になりますし、今後も、この仕組みを使ったAIや自動診断システムなどはどんどん大量生産されていき、身近になっていくでしょうし、そういう意味でも、このような解析方法があることを知っていると知らないでは、多分「見える世界」が変わってくると思います。

1. 例題提示：練習時間と技能習得の関係

あることを習得するには、たぶんそれを練習することが必要と思われます。では実際に、何人かに練習をしてもらい、その後、その技能を習得したかどうか、調べてみます。「あること」とは、例えば「自転車に乗る」でも良いし、幼児なら「両足で歩ける」でも良いし、「あるフレーズをピアノ（鍵盤）で演奏する」でもいいし... まあなんでも良いです(^^; それを、「何時間練習したか（何日練習したか）」と「その技能を習得できたか？（できなかったか？）」を調べ、表にまとめます。たとえば、


------------------

練習時間 習得(1/0)
 17.25	 1
 2.84	 0
 7.16	 1
 2.59	 0                                                           
 .....
------------------

のように、それぞれの人の「練習時間(実数)」と「習得したか否か（1:習得、0:未習得）」のデータを並べていきます。練習時間順に並び変えたExcel データをlogistic.xls に入れておきます。このデータの散布図は

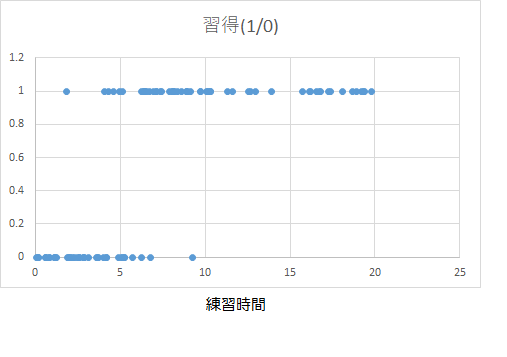
となります。このデータから「練習時間」と「習得の確率」の関係（の式）を求め「練習時間が習得に関係しているか？とか、練習時間を長くすると習得の可能性が高まるのか？とか、何時間くらい練習する必要があるのか？とか...」そういうことを見出そう、というのがこれから行う「ロジスティック回帰分析」です。

データをそのまま散布図で描いても、何を分析すればよいのかわかりにくいと思いますので、練習時間を階級幅１で階級で区切って、度数分布表にしてみましょう。ここでは四捨五入（0～0.5, 0.5～1.5, 1.5～2.5, ...）して、その範囲の練習時間の人数と習得者数・習得率（習得者数/人数）をまとめてみましょう。すると、


------------------------------

時間	人数	習得者	習得率
0	9	0	0
1	7	1	0.142857143
2	10	0	0
3	5	0	0
4	7	4	0.571428571
5	6	1	0.166666667
6	11	10	0.909090909
7	5	5	1
8	10	9	0.9
9	4	3	0.75
10	5	5	1
11	2	2	1
12	3	3	1
13	1	1	1
14	0	0	不定(N/A)
15	1	1	1
16	5	5	1
17	2	2	1
18	3	3	1
19	4	4	1
------------------------------

となり、「練習時間」と「習得率」のグラフは、

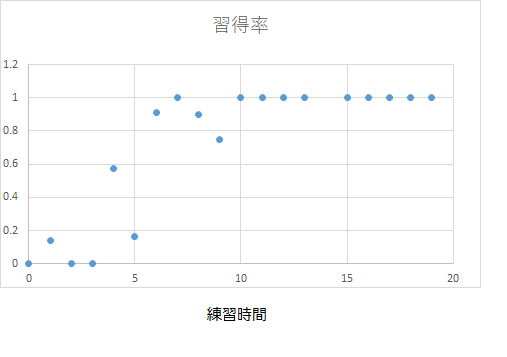
となります。もし、十分多くの人数で調べたのなら、その時間の習得者の人数/その時間の人数（習得率）は、その時間の「習得の（経験的）確率」とみなすことができるでしょう。このグラフを単純な数式で表現できれば、「練習時間と習得の確率」の関係を定式化できそうです。

しかし、この関係は「直線にはならない」ことは自明かと思います。もし直線のグラフだと、練習時間が大きい（100とか）ときに、習得率（確率）が１を超えてしまいます(^^; ですから、練習時間が小さいときには０に、練習時間が大きいときには１に近づく「曲線」でないといけません。そのような曲線の関数としてよく使われるのが、「ロジスティック関数（シグモイド関数＝S字の関数）」と呼ばれる、\[ \frac{1}{1+e^{-x}} =1/(1+\exp(-x)) \] という式で、グラフは

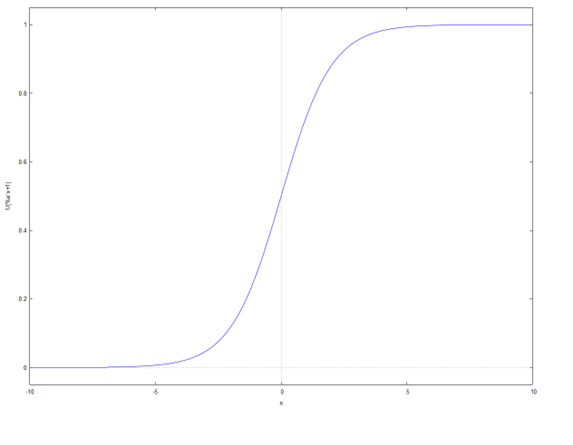
となります。\(x=0\)あたりで関数の値が多くく変化していきます。これを左右に動かしたり、横に引き延ばしたり縮めたりして、データを説明しよう、、というのが「ロジスティック回帰分析」です。つまり、練習時間\(x\)の時の習得の確率\(p(x)\)が、\[p(x) = 1/\{1+\exp [ - (a x + b ) ] \} \] になるとして、データから適切に、関数の形を決めるパラメタ\( a, b\)の値を求める、ということです。なおこの関数は、\(x=-b/a\)あたりで大きく変化し、\(a\)が大きいほど急速に(階段のように)変化するようになります。分析しにくい式のように見えますが、、確率\(p\)の代わりにオッズ\(p/(1-p)\)の対数を使うと、この式は、 \[ \log \frac{p(x)}{1-p(x)} = a x+b \] となるので、確率\(p(x)\)の代わりに、左辺に、そのオッズの対数（ロジット:logit）を使うと、右辺は「一次式」になるので、基本的には「線形回帰分析と同じ手法」が使えるようになります(グラフの形がS字になる関数はいろいろあるのですが、このロジスティック曲線（シグモイド曲線）の式を使うと、線形回帰と同じ形に変形できることから、この形の式がよく使われます)。細かいこと言うと、線形回帰分析では最小二乗法で「データをもっともよく説明する\(a,b\)の値を求める」のですが、ロジスティック回帰分析の場合には、「最尤度法（さいゆうどほう）」を使うことが多いです。これは、「与えられたデータが、得られる確率的に最も大きくなる\(a,b\)の組を求める」という手法です... なんか話がややこしくて難しくなってきましたが...(^^; 難しい計算は全部コンピュータが自動でやってくれますので安心してください(^^;;

いずれにしても、データから、「練習時間\(x\)」と「習得の確率\(p(x)\)」の関係を、２つのパラメタ\(a,b\) を含むロジスティック関数で表現し、２つのパラメタ\(a,b\)を具体的に求めてみましょう。

2. EZRによる、ロジスティック回帰分析

まず、EZRで、練習用のデータを読み込んでください(サンプルの大きさ＝データ数72個)。前に紹介した通り、練習用のデータはlogistic.xlsにありますので、ここからダウンロードしてください。もちろん、実際に解析したいデータが別にあれば、それを使ってもかまいません（と言うか、「実際のデータ解析」の場合には、当然そうします(^^;）。

[ファイル]→[データのインポート]→[Excelデータをインポート]で、教材ページのリンクからダウンロードしたテストデータ「logistic.xlsx」を選択します。そして、読み込んだデータを表示したり、散布図を書いてみて、入力データに間違えがないか、確認してください。確認が済んだら、いよいよ、このデータの解析に入ります。

[統計解析]→[名義変数の解析]→[二値変数に対する多変量解析（ロジスティック回帰）] を選んで下さい。なお、独立変数（説明変数）が１つでも２つ以上でも解析の仕方は全く同じですが、１つの場合と２つ以上の場合で用語を分ける時があります。例えば単回帰分析と重回帰分析。同じことですが説明変数が１つか複数かで「用語は」分ける時があります。説明変数が複数の場合「多変量解析」と言いますが、普通は１つの場合でも同じ解析ができます。今の場合簡単のため、「習得か非習得か（二値変数）」を１つの変数「練習時間\(x\)」で説明することを試みていますが、変数の個数が複数になっても（例えば、気温とかが加わっても）同じ解析ができますので、EZRでは「多変量解析」という名前のメニューになっています。なお、「名義変数」というのは、「数値としても意味がないもの」です。たとえば「習得したか否か」とか「性別」とか「国」とか「出身地」等のデータのことです。今は「習得したか否か」を0,1　で表しましたが、これは個数や量を表していませんので、「数値や量としての意味がない」ものです。そういう変数のことを「名義変数」と呼んでいます。

[目的変数] の[ ]をクリックしてから、[変数(ダブルクリックして式に入れる)]の「習得」をダブルクリックして、目的変数に[習得]を入れてください。

次に、[説明変数] の[ ]をクリックしてから、[変数(ダブルクリックして式に入れる)]の「練習時間」をダブルクリックして、説明変数に[練習時間]を入れてください。

あとはそのままで、[OK]を押せば、計算終了です。すると、次のような結果が表示されます。


==========================================================================
> #####二値変数に対する多変量解析(ロジスティック回帰)#####

> library(aod, pos=17)

> GLM.1 <- glm(習得.1.0. ~ 練習時間, family=binomial(logit), data=logistic)

> summary(GLM.1)

Call:
glm(formula = 習得.1.0. ~ 練習時間, family = binomial(logit), 
    data = logistic)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-2.71904  -0.30845   0.00638   0.34387   2.53923  

Coefficients:
            Estimate Std. Error z value   Pr(>|z|)    
(Intercept)  -4.8900     1.0914  -4.480 0.00000745 ***
練習時間      0.9226     0.1932   4.775 0.00000180 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 135.372  on 99  degrees of freedom
Residual deviance:  51.339  on 98  degrees of freedom
AIC: 55.339

Number of Fisher Scoring iterations: 7


> TempDF <- with(logistic, logistic[complete.cases(習得.1.0., 練習時間),])

> GLM.null <- glm(習得.1.0.~1, family=binomial(logit), data=TempDF)

> anova(GLM.1, GLM.null, test="Chisq")
Analysis of Deviance Table

Model 1: 習得.1.0. ~ 練習時間
Model 2: 習得.1.0. ~ 1
  Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
1        98     51.339                          
2        99    135.372 -1  -84.033 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

> vif(GLM.1)

> ###variance inflation factors

> odds <- NULL

> odds <- data.frame(exp( summary(GLM.1)$coef[,1:2] %*% rbind(c(1,1,1), 1.96*c(0,
+   -1,1))))

> odds <- cbind(odds, summary(GLM.1)$coefficients[,4])

> odds <- signif(odds, digits=3)

> names(odds) <- gettextRcmdr(c("odds ratio", "Lower 95%CI", "Upper 95%CI", 
+   "p.value"))

> odds
            オッズ比 95%信頼区間下限 95%信頼区間上限        P値
(Intercept)  0.00752        0.000886          0.0639 0.00000745
練習時間     2.52000        1.720000          3.6700 0.00000180
==========================================================================

まず、


==========================================================================
Coefficients:
            Estimate Std. Error z value   Pr(>|z|)    
(Intercept)  -4.8900     1.0914  -4.480 0.00000745 ***
練習時間      0.9226     0.1932   4.775 0.00000180 ***
---
==========================================================================

の部分に注目します。

これは、\[p(x) = 1/\{1+\exp [ - (a x + b ) ] \} \] 同じことですが、\[ \log \frac{p(x)}{1-p(x)} = a x+b \] の、\(b\)(切片)は-4.8900 で、練習時間\(x\)の係数\(a\)が0.9226だ、ということです。 \[a=0.9226\] \[b=-4.8900\] ですから、習得の確率\(p(x)\)は、 \[ p(x) = 1/\{1+\exp [ - (0.9226 x + (-4.8900) ) ] \} =1/\{1+\exp(- 0.9226 x + 4.8900 )\} \] 同じことですが、 \[ \log \frac{p(x)}{1-p(x)} = 0.9226 x - 4.8900 \] ということです。ちなみに、\[-b/a = 5.300 \]なので、習得率は、練習時間\(x=5.3\)、つまり５付近で大きく変わることがわかります。

イメージつかむために、前に提示したサンプルデータの散布図や、度数分布に区切った習得率のグラフと、ロジスティック回帰分析で求めた関数のグラフを重ねて描いておきましょう(関数のグラフなどは、普通はグラフを描くソフト(gnuplot等)や演習室に入れてあるソフトならwxMaximaを使えば一番簡単ですが、Excelでも与えられた数式の関数表を作ってグラフ表示することは簡単にできます。数式のグラフは、現在では人間が(数学の知識を駆使して)描くものではないでしょう(^^;)。

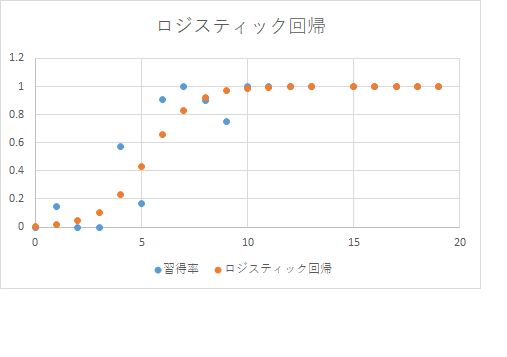
なお、この値は「サンプルの回帰分析での値」です。では、サンプル内だけでなくランダムサンプリングをした元の「母集団」ではどうか？　そういう検定も、EZRでは自動的に行ってくれます。そして、右端のPr(>|Z|)は、p-value,つまり、もし、切片や練習時間の係数が０だとしたときに（つまり、練習時間により習得の確率が変化しないと仮定したときに）、今のようなデータが得られる確率を意味しています。今の場合、十分に小さな値ですから、\(a,b\)は0ということはないだろう（得られた\(a,b\)の値は、多分意味を持つだろう、と推測できます。また、「Std. Error」とは Standard Error日本語では「標準誤差」の意味です。なお標準誤差とは「標準偏差」の意味ですから、およそ68%(68.24%)信頼区間の範囲を意味しています。もし、90%信頼区間を知りたければ、その1.645倍、95%信頼区間を求めたければ1.960倍、99%信頼区間を求めたければ2.576倍です。\(a\)(練習時間の係数)の標準誤差が\(0.1932\), \(b\)(切片)の標準誤差が\(1.0914\)と表示されていますから、必要なら、
　68%信頼区間: \( a= 0.7294～1.2258, 　 b= -5.981～-3.799, 　 -b/a= 3.40～8.20 \)
　90%信頼区間: \( a= 0.6048～1.2404, 　 b= -6.685～-3.095, 　 -b/a= 2.49～ 11.05\)
　95%信頼区間: \( a= 0.5439～1.3013, 　 b= -7.029～-2.751, 　 -b/a= 2.11～12.92 \)
　99%信頼区間: \( a= 0.4243～1.4209, 　 b= -7.705～-2.075, 　 -b/a= 1.46～18.16\)
と求めることもできます。まあ、b/a（習得度を大きく変える練習時間）は、およそ５程度、70%くらいの確率で(68%信頼区間で)３～８くらい、99%信頼区間なら1～１８程度...ということくらいは言えるかもしれませんね...　まあ、計算結果の数値は細かく出せますが、「誤差が大きい」ですから、結果としては、有効数字を意識しておおまかに表現すると良いでしょう。

最後の


==========================================================================
> odds
            オッズ比 95%信頼区間下限 95%信頼区間上限        P値
(Intercept)  0.00752        0.000886          0.0639 0.00000745
練習時間     2.52000        1.720000          3.6700 0.00000180
==========================================================================

は、単位\(x\)あたりのオッズ比を示しています。つまり、練習時間(\(x\))を１増やしたとき、習得のオッズは何倍になるか、という量です。練習時間のオッズ比が2.52ですから「練習時間を増やしたほうが、習得の確率（オッズ）が上がる」ことを意味しています。なお、サンプルでオッズ比は2.52ですが、ランダムサンプリングでデータを取った元の母集団では、たぶん（95%位の確率で）1.72～3.67くらいだろう（少なくともオッズ比が1ということはないだろう。母集団のオッズ比が1だとしたら(練習時間と習得が無関係と仮定したら)今のデータが得られる確率=P値は、0.00000180(\(1.8 \times 10^{-6}\))なので、そんな確率の低い出来事が今回たまたま起こったとは考えにくいだろう＝練習時間と習得率が無関係と言うことはありえないだろう）ということになります。

つまり、「与えられたサンプルデータ」から、は、習得の確率\(p(x)\)は、 \[ p(x) = 1/\{1+\exp [ - (0.9226 x + (-4.8900) ) ] \} =1/\{1+\exp(- 0.9226 x + 4.8900 )\} \] とモデル化できるが、「母集団」では、その係数は、それほど（４桁とか）の精度を持たず、もし95%信頼区間で議論するなら、a=0.5～1.3くらい、b=-7～-2くらいの範囲内であり、習得率を大きく変化させる練習時間は、２～１４程度であろう、と予想できます。なお、「練習時間を増やせば習得率が上がる（練習時間を増やすと習得のオッズが上がる）」度合いは、オッズ比の95％信頼区間が1.72～3.67くらいなので、少なくともオッズ比は１ではないだろう（練習時間を増やせば習得のオッズが上がる）し、もし練習時間と習得率が無関係と仮定すると：練習時間の係数が=0と仮定すると（帰無仮説）、現在のデータが得られる確率p-value(P値)が0.00000180なので、そんな確率の低い出来事が今回たまたま起こったとは考えにくいだろう、つまり「練習時間が習得には、相関がある」ということが言え、多分「練習時間を増やすことにより習得率が上がる（因果関係）」があることも期待できるでしょう（なお、単なる期待ではなく、因果関係があるかどうかを調べるには、調査データではなく、少なくとも実験（あるいは観察データの場合には、実験とみなせるような前処理）をする必要があります）。

3. EZRによるロジスティック回帰分析(データが少ない場合(20個))

先ほどは、データがある程度取れる場合（度数分布が得られる程度）について解析してみましたが、ついでに、「データ数があまりとれなかった場合（度数分布が描けないほど少ない）場合」についても、やってみましょう。テストデータとしては、先ほどのデータから、さらにランダムに20個のデータをとってきました。これをサンプルデータとして解析してみましょう。


練習時間　習得(1/0)
　 3.65　　0
　10.19　　1
　 6.43　　1
　 4.97　　1
　 0.15　　0
　 5.11　　0
　 1.24　　0
　 8.08　　1
　 3.98　　0
　 8.88　　1
　16.58　　1
　 9.14　　1
　 1.2 　　0
　18.1 　　1
　 1.1　　 0
　 4.88　  0
　 6.24　  0
　10.3　   1
　 2.58　  0
　 0.58　  0

この場合、


> #####二値変数に対する多変量解析(ロジスティック回帰)#####

> GLM.4 <- glm(習得.1.0. ~ 練習時間, family=binomial(logit), data=Dataset)

> summary(GLM.4)

Call:
glm(formula = 習得.1.0. ~ 練習時間, family = binomial(logit), 
    data = Dataset)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-1.40526  -0.16283  -0.02528   0.07803   1.77193  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  -8.6070     4.8340  -1.781   0.0750 .
練習時間      1.4629     0.8461   1.729   0.0838 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 27.5256  on 19  degrees of freedom
Residual deviance:  7.1762  on 18  degrees of freedom
AIC: 11.176

Number of Fisher Scoring iterations: 8


> TempDF <- with(Dataset, Dataset[complete.cases(習得.1.0., 練習時間),])

> GLM.null <- glm(習得.1.0.~1, family=binomial(logit), data=TempDF)

> anova(GLM.4, GLM.null, test="Chisq")
Analysis of Deviance Table

Model 1: 習得.1.0. ~ 練習時間
Model 2: 習得.1.0. ~ 1
  Resid. Df Resid. Dev Df Deviance    Pr(>Chi)    
1        18     7.1762                            
2        19    27.5256 -1  -20.349 0.000006451 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

> vif(GLM.4)

> ###variance inflation factors

> odds <- NULL

> odds <- data.frame(exp( summary(GLM.4)$coef[,1:2] %*% rbind(c(1,1,1), 1.96*c(0,
+   -1,1))))

> odds <- cbind(odds, summary(GLM.4)$coefficients[,4])

> odds <- signif(odds, digits=3)

> names(odds) <- gettextRcmdr(c("odds ratio", "Lower 95%CI", "Upper 95%CI", 
+   "p.value"))

> odds
            オッズ比 95%信頼区間下限 95%信頼区間上限    P値
(Intercept) 0.000183     0.000000014            2.38 0.0750
練習時間    4.320000     0.822000000           22.70 0.0838
==============================================================

となりました。重要なところを抜粋すると、


==============================================================
Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  -8.6070     4.8340  -1.781   0.0750 .
練習時間      1.4629     0.8461   1.729   0.0838 .

> odds
            オッズ比 95%信頼区間下限 95%信頼区間上限    P値
(Intercept) 0.000183     0.000000014            2.38 0.0750
練習時間    4.320000     0.822000000           22.70 0.0838
==============================================================

データ数が少ないので（サンプルの大きさが小さいので）、ゆらぎがおおきいかもしれませんね(^^;　それでも、 \[a=1.4629 (標準誤差: 0.8461) \] \[b=-8.6070 (標準誤差: 4.8340) \] が得られますが、習得の確率が大きく変化する\(x\)の値は\[-b/a = -5.8835\]ですが、\(a,b\)の誤差を見るとかなり誤差が大きいので、あまりはっきりとしたことは言えません。なお、練習時間の係数のp-valueは0.35程度、つまり、「もし練習時間の係数が０だとしたら、このデータが得られる確率は8.4%程度、はっきりした事は言えないけど、練習時間の寄与がある可能性があるのかも知れない（8.5％らいの確率で、無いかもしれない）」、程度のことは言えそうです。また、オッズ比（練習時間１変化させた時の、オッズの比）もサンプル内では4.32と、１より大きいですが、95%信頼区間だと、0.822～22.70 つまり、１を下回る可能性も（8%以上の確率で）残ります。で、このデータだけでは、「練習時間を増やせば習得率が上がると示されたとは言えない」ですが、当然「練習時間と習得率に関係が無いことが示されたわけでもない」です。「どちらかと言えば、練習時間が習得率に関係している可能性が高いが、データ数が少ないので、良く分からない」が妥当なところでしょう。データ数が少なければ確かなことは言えませんが、だからと言って、何も言えない（調査が無意味だった）わけではなく、可能性に気がつくきっかけにはなりますので、「今後データを増やして調べることが大切かもしれない」ということは言えそうです。確率の数値を見ながら、皆さんが、妥当な「可能性の程度を判断」をすれば良いと思います。形式的に（＝マニュアルに従って）有意水準を超えるか超えないかで、有意とか有意でないと、短絡的に２つに１つの誤った２分法による判断（デジタル的に判断）するのは、誤りの原因になります。確率（連続量）に基づき、正しくアナログ的に判断しましょう。

4. EZRによるロジスティック回帰分析(極端にデータが少ない場合(10個))

さらにデータが少ない場合、１０個しかデータが取れなかった場合の解析をしてみます。


練習時間  習得(1/0)
 3.65	  0
10.19	  1
 6.43	  1
 4.97	  1
 0.15	  0
 5.11	  0
 1.24	  0
 8.08	  1
 3.98	  0
 8.88	  1

この場合、


==============================================================
> #####二値変数に対する多変量解析(ロジスティック回帰)#####

> library(aod, pos=17)

> GLM.1 <- glm(習得.1.0. ~ 練習時間, family=binomial(logit), data=Dataset)

> summary(GLM.1)

Call:
glm(formula = 習得.1.0. ~ 練習時間, family = binomial(logit), 
    data = Dataset)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-1.23997  -0.12354  -0.00011   0.01165   1.29901  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  -15.451     16.286  -0.949    0.343
練習時間       3.052      3.259   0.937    0.349

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 13.8629  on 9  degrees of freedom
Residual deviance:  3.3546  on 8  degrees of freedom
AIC: 7.3546

Number of Fisher Scoring iterations: 9


> TempDF <- with(Dataset, Dataset[complete.cases(習得.1.0., 練習時間),])

> GLM.null <- glm(習得.1.0.~1, family=binomial(logit), data=TempDF)

> anova(GLM.1, GLM.null, test="Chisq")
Analysis of Deviance Table

Model 1: 習得.1.0. ~ 練習時間
Model 2: 習得.1.0. ~ 1
  Resid. Df Resid. Dev Df Deviance Pr(>Chi)   
1         8     3.3546                        
2         9    13.8629 -1  -10.508 0.001188 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

> vif(GLM.1)

> ###variance inflation factors

> odds <- NULL

> odds <- data.frame(exp( summary(GLM.1)$coef[,1:2] %*% rbind(c(1,1,1), 1.96*c(0,
+   -1,1))))

> odds <- cbind(odds, summary(GLM.1)$coefficients[,4])

> odds <- signif(odds, digits=3)

> names(odds) <- gettextRcmdr(c("odds ratio", "Lower 95%CI", "Upper 95%CI", 
+   "p.value"))

> odds
                オッズ比 95%信頼区間下限 95%信頼区間上限   P値
(Intercept)  0.000000195        2.67e-21        14200000 0.343
練習時間    21.200000000        3.56e-02           12600 0.349
==============================================================

となりました。重要なところを抜粋すると、


==============================================================
Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  -15.451     16.286  -0.949    0.343
練習時間       3.052      3.259   0.937    0.349
...

> odds
                オッズ比 95%信頼区間下限 95%信頼区間上限   P値
(Intercept)  0.000000195        2.67e-21        14200000 0.343
練習時間    21.200000000        3.56e-02           12600 0.349

==============================================================

です。さすがにここまでデータ少ないと、何も主張できそうにありませんね。「練習時間と習得率が全く無関係であったとしても、ランダムサンプリングによるバラツキで、この程度偏ったデータが得られる確率が30％以上ある(p-value>0.3)」、ということですから。もちろん、サンプルデータだけからいろいろな推定値（最適なロジスティック曲線）を計算はできますが、その値の揺らぎ（統計誤差）が大きいですから、「計算結果には殆ど意味はない」でしょう。丁度、前に「一様分布の頻度分布を見ると、データ数が少ない時は意味ありげに（何か傾向があるように）見える」と言うことを体験しましたが、丁度それに対応しています。何もなくても何かあるように見えるような状況（データ数）では、サンプルデータから何かを主張することは危険ですし大抵の場合、全くの誤りになります。素直に「このデータからだけでは、何も分からない（何か情報を得るためにはもっとデータを集めることが大切）」と判断することが大切です。

5. まとめ。

どうですか？　かなりややこしかったかもしれませんが、「連続値の値（大小）から、何かを判定する」場合には、このような分析や議論が、汎用的に使えますので（実際に様々な場面で使っていますので）、「こういう解析が簡単にできるんだ」ということを知っておくと、役に立つときが来るかもしれません。また、このような（非線形の回帰分析ですから）比較的高度な解析でも、基本的には「２項検定や、サンプルから母集団の平均値や推定する方法(１標本ｔ検定)」と殆ど同じ手順や同じ考え方（p-valueや信頼区間）が使われている、ということを感じていただければ良いと思います。そのことが理解できれば、もっとややこしい（高度な）解析も「難しい計算はコンピュータに任せて」コンピュータ出力（計算結果）から、必要な情報を読みとることにより、様々な解析を、簡単に行うことができるようになれると思います。なお、「このような道具(コンピュータと統計ソフト)を使わないと」ロジスティック回帰分析などは、かなり高度な数学的素養と計算能力が必要となりますので、「昔は」専門家しかできない解析だったかもしれませんし、数学的な素養のない人だと、知らない・理解できない人が多かったかもしれません。そのような、過去の時代には、こういう高度なデータ解析は、専門家レベルとか大学院レベルとか位置づけられていたかもしれません。しかし今は、「コンピュータが身近にあり、無料で簡単に使える統計ソフト(例えばEZRなど)がある」し、教材も「ネット上にいくらでもある」ので、ちょっと気の利いた高校生くらいなら、(理系文系関係なく)簡単に自学自習でロジスティック回帰分析くらいならできてしまう時代である(そして、この講義を受けた皆さんも、ロジスティック回帰分析程度なら、普通にできて、使えてしまう)、ということを、知っておくとよいと思います。

さらに「実用的な」解析として、線形回帰もロジスティック回帰も「説明変数（独立変数）」を２つ以上に増やす「多変量解析」というものもあります。例えば、体重を、身長と性別という２つの要因から説明できるか？」などが既に提示した練習データでここ見ることができる例です。他にも、様々な要因や結果などを調査して、「どの要因がどれだけ効いている（あるいは無関係）と考えられるか？というのを多変数の一次式やロジスティック関数でモデル化し、その係数が０なら無関係。０で無ければ関係がある... という形で、関係の無い要因を自動的に排除していき、関係しそうな要因のみを選び出して、その要因で結果を説明する（モデル化する）」というようなことも、EZRを使うと、ほとんど自動的にできますし、「やり方は、今まで紹介した,１つの説明変数（独立変数）の場合とほとんど同じ」ですし、詳しい具体的な操作方法の説明や結果の読み取り方は、既に紹介したサイト等にもありますので、必要な方は、必要なときに参照して、チャレンジしてみてください。本授業で基礎を学んだみなさんなら、すぐにそのような解析もできるはずです。なお、このような解析は「一昔前は、数学もコンピュータも詳しい人しかできなかった」ので、とても難しい（大学院レベル）のことのように思っている古いセンスの人もいるかも知れませんが、現在の文明の利器（EZRや、高機能な統計ソフト）を使えば（高校生レベルでも）簡単にできることですし、しかもEZRを使えば「誰でも無料で」そのような処理を行う環境を、自分のPC(Windowsなら楽)に作れ、どこでもそのような処理を「自分が」できる能力を持つことができる時代になっています。