
暗号... と聞くと、皆さんは何を思い出します? ドイツ軍の暗号機エニグマと、それを破り第二次世界大戦の集結へと導いたアラン・チューリングの話が頭に浮かんだら、いいですね(^^;;
最近になるまで「暗号」というのは一部の人が使う、そして大抵の場合「争い事(戦争)」において使われる技術でした。昔の日本においても、他の土地の人からの侵略に対抗するために、他の土地の人にはわからないように、使う言葉を意図的に変え、それが(他の地方の人には何を言っているのかわからないほどの)一部の方言の始まりとも言われています。そのような方言は、ある意味、戦争が原因の「暗号化」とも言えるかもしれません。
暗号が必要になる(あるいは暗号が有効である)のは、特定の相手だけに情報を伝えたいが、伝える媒体としては「公共(誰でも使える)あるいは、情報を伝える経路で、情報が漏れる(盗聴される等)可能性がある」ものを利用する場合です。初めから「自分と相手しか」繋がれていなければ「暗号」は必要ありません。「手紙」などで情報を伝えていた時代には、手紙を読まれ無いために「封書、封印」が使われ、それでも読まれた場合に備え「暗号」が使われ始めました。アナグラムも(主には言葉の遊びですが)暗号の一種として使われることもありましたが、それほど一般的ではありませんでした。第二次世界大戦の時に「無線通信(ラジオ)」が普及します。戦争で遠くにいる味方の部隊が「タイミングを合わせて一斉攻撃する」のに無線通信が使われましたが、これは受信機があれば誰でも受診できてしまいますので「暗号文」で送ることが一般化し、ドイツ軍は当時解読不能と言われるほど強力な暗号を「エニグマと呼ばれる機械」を利用して使います。この時代でも暗号は「主として戦争に使われるもの」でしたから、その解読も軍事行動の一環として行われ、英国ではMI6がアラン・チューリングなどの学者を雇い、最高の軍事機密として、暗号の研究が行われます(そしてチューリングはエニグマの暗号を解読しますが、死後もそれは(MI6の盗聴の道具として利用され)英国最高の軍事機密として扱われます)。そしてチューリングが考えていた(暗号解読もする)機械が、のちに「デジタルコンピュータ」と呼ばれるものへと発展していきます。
1950年以降の「コンピュータ」の時代、最初は「ビルの一室にあるコンピュータの操作装置」から操作する時代でしたし、「部屋に入ること自体が機密確保」でしたし、そもそもコンピュータを使える人も限られていましたので「軍事用の暗号を解読する以外には」、コンピュータで暗号を使う必要がありませんでした。1960年ごろからコンピュータは市販され「多くの人が、1台のコンピュータを共用して使う時代」になると、「自分のデータと他人のデータ」を区別するために、「アカウントとパスワード」が用いられ始めます。その時代、「真実を求める、知識を増やす」ためにコンピュータを使う「学者・研究者」は、これに反発しますが「知識を独占する、データを所有する」ことにより「経済的利益や軍事的利益、争いにおける優位性」を確保するためにも「コンピュータ」が使われ始めると、「アカウントとパスワード」でデータを守ることが一般的になっていきます(ここには思想上の違い(理想のあり方)などもあり、パスワードを付けない、無効化する、という運動も生まれます)。この「パスワードで守る」というのが、コンピュータ利用における「暗号化」の始まりかもしれません。
さらに進み、コンピュータネットワークの時代(インターネットの時代)に入ると、コンピュータは「機密が確保された部屋にある」ものではなく「どこからでもネット経由で利用できるもの」へと変貌していきます。それに伴い、コンピュータ自体は機密が確保されている部屋に設置されていても「データや、利用は、どこからでも(誰でも)できる」という、いわば無線通信やラジオのような状況になります。また、コンピュータは学者や研究者が、純粋に「真実を求める、知識を増やす」ためだけに使うのではなく、「様々な経済活動にも使うもの」へと変化していきましたので、「情報を守る」ことは「財産を守る」ことと同義になり、必要不可欠なものへと変貌していきます(ノーパスワードでの利用はあり得ない、という時代になっていきます)。そして、「暗号化」は現代社会の仕組みを守る「現代文明の維持に必要な、根幹の技術」へと変貌しています。
しかし「高度な暗号化技術」は「高度な軍事技術」としての側面があるため、例えば米国では1992年まで「高度な暗号技術」は「強力な輸出規制」がおこなれていました。2000年頃から規制緩和されましたが「高度な軍事技術」でもあることには変わりありませんので、現在でも米国の輸出規制はあります。しかし、「暗号化」は軍事だけでなく「情報化社会の基盤」になるものですから「国際的に高度な暗号化技術が開発され、(フリーソフトとして)公開され、また(国際規格として)標準化され」それが世界中に普及しています。
まず最初に、皆さんが既に使っている「アカウントのパスワード」の管理方法の話から始めましょう。
皆さんの多くは、それ以外にもネットサービスを利用するために、既に多くのアカウントを持ち、利用していると思います。アカウント(ID)は本人を特定するための識別記号(名前)であり、本当に本人かどうかを確認(認証)するために「パスワード」が求められます。
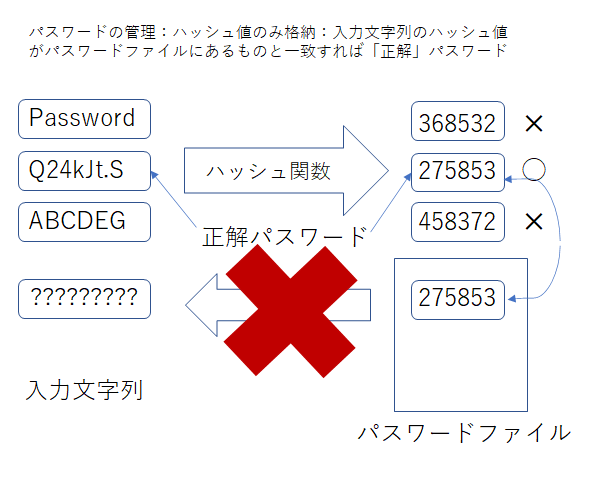
認証システムは、「認証画面において、利用者が入力した文字列」が「正しいパスワードか誤りか」を判定する必要があります。ですから、正誤を判定するために「システムに、正しいパスワードが保管されているのではないか?」と想像する人が多いかもしれません(^^; しかしそれは誤りで、実は、まともな認証システムであれば「正解パスワード自体は、何処にも保管されていない」のです(パスワード自体を保存しているシステムは「セキュリティ的にはまともで無い」です。キーワード「スマホ 盗難 全財産」等で最近のニュースなどを検索するのも良いでしょう)。ですから、自分のパスワードを忘れた場合「管理者に問い合わせてもパスワードはわかりません」し、そのような場合には「初期化(管理者が決めたパスワードを新たに設定し、それを利用者に知らせる)」という手続きが取られます。では、認証システムは「正解パスワードを知らずに」、入力された文字列が正解パスワードかどうか、どうして判定できるのでしょう?
認証システム内に「パスワード判定に利用する、通称「パスワードファイル」」はありますが、ここに保存されているのはパスワードそのものではなく、個々の「パスワードの文字列を数字化(コード化)したものに対して『ある決められた演算をした答え(=あとで述べるハッシュ値)』」が入っています。
「パスワードそのものを保存しない」のは、仮に「パスワードファイルを盗まれても、ただちにパスワードが知られるわけではない」ようにするためです。
ここに使われる『ある決められた演算』というのが曲者で、「問題(A)から答え(B)を出すのかは簡単」だが「答え(B)から問題(A)を推測するのは不可能」という「一方通行の演算」です。「一方通行の演算」は正式には「一方向性関数」と呼ばれます。また、答えの数値の桁数を決められた範囲に収める、という現実的に必要な機能も同時に含め、「(一方向性・暗号学的)ハッシュ関数」と呼ばれることもあります(実際に使われるハッシュ関数には、MD5,SHA-1,SHA-2,SHA-3などがあります。なお"hash" とは、ハッシュドポテトなどの「ハッシュ」と同じ言葉で、「細切れにしてごちゃまぜにする」というような意味の英単語です。ハッシュ関数は、入力のビット列を、細切れにして、ぐちゃぐちゃにまぜる、最後に定められた長さだけ切り出すような、まるでジャガイモをハッシュドポテトにするような演算をします。そしてその答え(大きさの決まったハッシュドポテトのようなもの)をハッシュ値と言います)。

・A(文字列) → B(ハッシュ値)(簡単)
・A(文字列) ← B(ハッシュ値)(困難・あるいは不可能)
ここでは、「入力(A)に対し、決められた一方通行の演算をした答えを、ハッシュ値(B)と呼ぶ」と思ってください。そして、この値が、元の入力(A)の全体の性質を反映した、暗号のような値になります。
「パスワードファイルには、正解パスワードそのもの(A)ではなく、正解パスワードのハッシュ値(B)だけが保存」されています。
そして、パスワード要求に対して「文字列(A)」が入力されると、システムはAに対して「決められた一方通行の演算」を行い、その答えが「パスワードファイルに記録されている正しいハッシュ値」と一致するか否かで、「正しいパスワードか、誤りか」を判定しています。なお、「ちゃんとした認証システム」の場合、この方法でパスワードの真偽を判定していますので、「パスワードファイルが盗まれた(流出した)」だけでは、まだ「パスワードのハッシュ値(B)が流出した」だけで「パスワードそのもの(A)が盗まれたわけではない」ことになります。
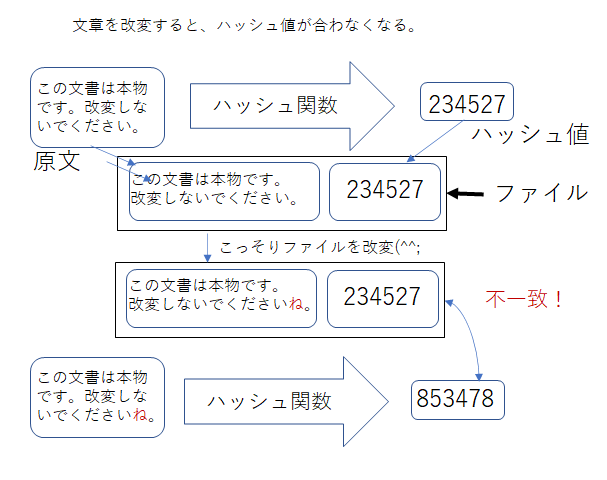
パスワードの管理に使われる「一方向性関数(ハッシュ)」の仕組みは、パスワード以外にも、一般に「入力されたデータが正しいかどうか」の確認に使えます。パスワードのような比較的短い文字れるだけでなく、長い文書全体とかを入力にして、ハッシュを求めることもできます。
実際によく使われるハッシュ関数は「入力の長さは無制限、出力の長さは固定」「入力の僅かな差が、出力の大きな違いになる」「情報が欠落しているため、原理的に逆演算は不可能(ハッシュ値から元の入力を求めることができない:一方向関数)」という性質を持ちます。また、複数の入力が同じハッシュ値を持つことがありますが、十分にハッシュ値の長さを十分に長くすると、偶然同じハッシュ値が得られる確率が極めて低くなります。この性質を利用すると「ある文書が、(第三者により)改ざんされていないかどうか?」を判別する機能を実現することができます。つまり「正しいかどうか?(改ざんされていないかどうか?)」という「認証の機能をデジタル化」することができます。ただし、単にハッシュ値を付加するだけでは、ハッシュ値も一緒に改ざんすることが可能になるため、実際には、後で述べる暗号化の技術も組み合わせた「デジタル署名(デジタル証明書)、電子署名(電子証明書)」の形で用いられます
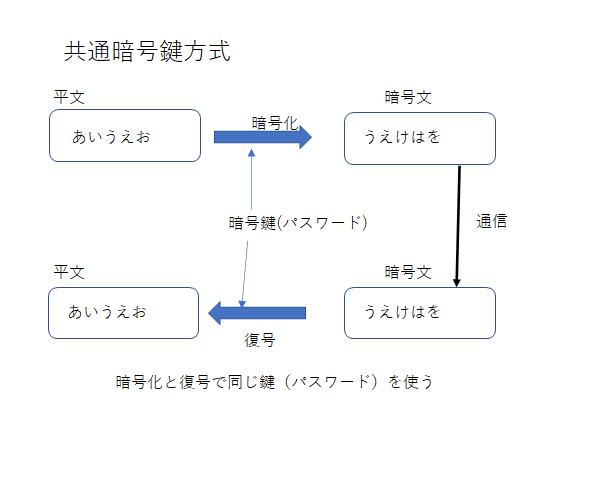
では次に「暗号」の話に進みます。「元の文章(平文)を、他の者が読めない形(暗文)にして伝達する」技術を「暗号化」の技術と言います。簡単な暗号化の仕組みは、たとえば、「元の文書(平文)」と「暗号化鍵(パスワード)」により決まるある演算をした答えを「暗号文」とする方法です。たとえば(古典的なシーザー暗号の場合)、ひらがなの文書を「五十音順に1文字後ろにずらず(あ->い、い->う....)」などと変換した文を暗号文とする、という方法です。この場合「1文字後ろにずらず」ということが暗号化鍵(パスワード)に相当します。同じ方法で鍵を「2文字後ろずらす」にすると、別の暗号文になります。この場合、逆の変換、つまり「1文字前にずらす」という変換をすると、「暗号文から元の文(平文)に元すこと(復号と言います)」ができます。実際はもっと複雑な演算をしますが、「平文」に対して「鍵(パスワード)」よる演算を行い「暗号文」を作り、「暗号文」から同じ「鍵(パスワード)」を使って逆演算をすることにより「平文」に戻すという仕組みは、基本的に同じです(エニグマも基本的には同じです)。この方式は「暗号文を作るための鍵(暗号化鍵)」と「暗号文を平文に戻すための鍵(復号鍵)」が同じため「共通暗号鍵方式」と呼ばれています。まあ「パスワードで暗号化し、戻す時には、暗号化した時と同じパスワードを使う」と言っても良いと思います。MS-Office等にも組み込まれていて、例えばWordで作った文章を「パスワードで暗号化」して、それをメールなどで送れば、途中でそのファイルを盗まれても、パスワードを知らなければ内容は秘密のままになります。この暗号方式を使う場合には「読む資格を持った人だけが、パスワード(共通暗号鍵)を知っている」という状態を維持することが必要になります。
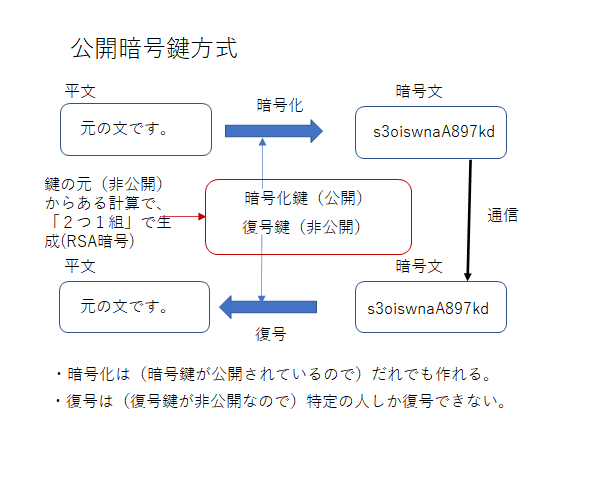
共通暗号鍵方式は「暗号化に使う鍵(暗号化鍵)」と「平文に戻すために使うう鍵(復号鍵)」が同じでしたが、一方向性関数の理論を発展させると、これを「異なる鍵」にすることが可能であることが見出されました。「暗号化に使う鍵(暗号化鍵)」を「公開」し、「平文に戻すために使う鍵(復号鍵)」は「秘密」にすることにより、「誰でも暗号文を作ることができる」が「平文に戻せるのは、秘密鍵を知っている人だけ」という暗号化が実現されます。暗号文を作るための鍵(暗号化鍵=公開鍵)を公開するので「公開暗号鍵」方式と呼ばれますが、もちろん暗号文を平文に戻せるのは「公開しない復号鍵=秘密鍵を持っている人だけ」です。
このような仕組みは、整数論のフェルマーの小定理を利用した演算で具体的に作ることが可能であることが分かり、Rivest,Shamir, Adlemanにより具体的に「2つの素数」が「鍵の素」として使う方法が提唱されます(RSA暗号)。詳しい話は(高校数学+α程度の内容ですがややこしく話が長くなるので)省略しますが、簡単に概略のみ説明します。まず2つの素数を\(p,q\)と書き、これを「公開しない鍵(秘密鍵)」とします。この積を\(n\)と書き、これを「公開する鍵(公開鍵)」とします。当然\(n=p q\)です。この\(n\)を「 暗号化するための鍵(暗号化鍵=公開鍵)」として使います。これを公開すれば「誰でも暗号文が作れる」ようになります。ところで元の文を暗号鍵\(n\)で暗号化するとき、「\( A \rightarrow B \)」の演算は公式で簡単にできるが、問題と答えを逆にした「\( B \rightarrow A \)」の公式が存在しない(だから簡単には演算できない)関数(一方向性関数)を使います。ですから暗号化鍵\(n\)を知れば「暗号化はできる」けれどその鍵を知っていても「平文に戻すこと(復号)はできない」ことになります。
ところが、この暗号化の一方向関数として「ある種の演算」を使うと、\(n\)の元になった2つの素数\(p,q\)を使えば元に戻せる、ということが可能になります(そのような一方向性関数を使います)。具体的には、ある種の剰余演算(モジュロ演算)を使い、その中でフェルマーの小定理を応用した計算(中国人剰余定理とも呼ばれる)をすると、そういうことが具体的にできます(RSAと呼ばれています)。暗号鍵を作る人(暗号を復号して読む人)は、\(n\)の元になった2つの素数\(p,q\)を知っていますから、これが「復号するための鍵(復号鍵=秘密鍵)」になります。こちらは公開せず秘密にしておきます(秘密鍵と呼ばれます)。つまり、2つの素数 \( p,q \)の値が「秘密にする復号鍵」で、その積の値\(n\)が、公開する暗号化鍵になります。
ところで... \(n=pq\)で、\(n\)は整数、\(p,q\)は素数なんだから、公開鍵の\(n\)から、中学校で教わった「素因数分解」の問題を解けば、秘密鍵\( p,q\) がわかるのでは? と思う人もいるかも知れません。実際、そうなんです。ただし、素因数分解の問題が「解ければ」です。\(p,q,n\)が比較的小さな数なら、中学生でも解けますが、大きな数の場合、素因数分解の問題を解くのは「極めて難しい問題」に早変わりします。候補となる数を持ってきて、割り切れるかどうかを判定し、割り切れない場合には別の数を... ということを繰り返すしかありませんので、少し大きな数(例えば100桁くらい)だと、多分余程運が良く無い限り手計算では不可能...というかコンピュータ使っても10年とかの短い時間では不可能でしょう。1000桁だとかなり高性能なコンピュータを使っても数千年とかの「短い時間」では不可能でしょう。10000桁の素因数分解になると、多分スーパーコンピュータ富岳を使っても、数百億年とかの「短い時間」で解くことは不可能でしょう。大きな数の素因数分解って、そのくらい「難しい問題」になりますので、「短い時間では解けない」として扱うことは、現実的です。つまり、公開暗号鍵方式は、 「大きな数の素因数分解の問題が、事実上解けない、という仮定」によって成り立っていることを知っておいてください。
# アニメ:サマーウォーズで、主人公の高校生が、電車で読んでいる本は量子コンピュータを使った素因数分解の仕方の本、誕生日の曜日当てで利用しているのがここでも名前だけ紹介したフェルマーの小定理を用いた剰余計算。長い数字を「問題」として計算しているのは素因数分解でしょう。大きな桁数の数の素因数分解の問題を主人公の高校生が解いて公開暗号鍵方式の暗号を破る、という設定と思われます。 まあアニメですから(^^;では次に、「無断で改変等」ができないようにする技術、デジタル署名等の技術について説明します。
公開暗号鍵の技術(暗号化用の鍵と複合用の鍵が異なる)は、「どちらの鍵を公開するか(暗号化鍵と府記号鍵のどちらを公開鍵としどちらを秘密鍵とするか)」を変えると、「本人が書いた文章か否か」を判別する、判子やサインの役目を果たすものにすることができます。
暗号の場合には
[平文」-(公開鍵) →「暗号」-(秘密鍵)→ 「平文」
でしたが、「平文」「暗号文」は、どちらも「文」ですので、これを入れ替えてみます。
[暗号文」-(公開鍵)→「平文」-(秘密鍵)→ 「暗号文」
こう考えると、「公開鍵で暗号文を平文に変換(復号)」できて、「非公開の秘密鍵で平文を暗号文に変換(暗号化)」することができます。つまり「
暗号文を作れるのは、秘密鍵(=暗号化鍵)を知っている特定の人だけ」で、「暗号文は、誰でも(公開鍵(=復号鍵)を使って復号し)平文にして読める」という機能が実現できます。
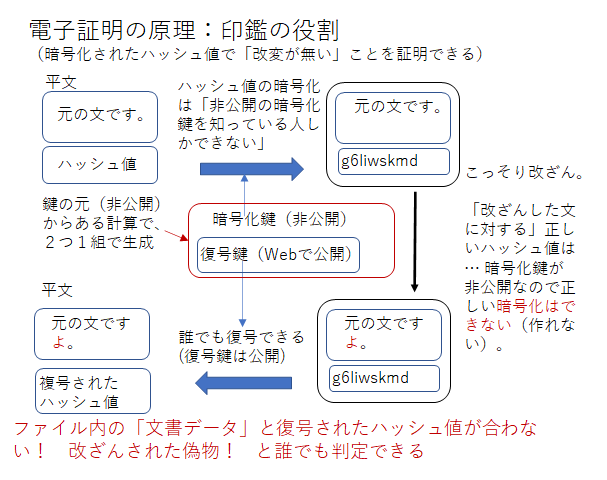
そこで、相手に送りたい「本文(原本)」のハッシュ値(定められたハッシュ関数=一方向性関数を用いて変換した値)を「秘密鍵で暗号化して」、「本文と暗号化されたハッシュ値を一緒に」送ります。受け取る人は、受け取った「本文」がありますから、そこから「ハッシュ値」を計算で求めることができます。また、「暗号化されたハッシュ値」も受け取りますから、それを公開鍵を使って平文に戻し「送信者が(暗号化して)送ったハッシュ値」を得ることができます。もし、本文(や暗号化されたハッシュ値など)が改ざんされていなければ、この「計算で求めたハッシュ値」と「送信者から(暗号化して)送られたハッシュ値」は等しくなります。もし両者が一致しなければ「送信者から送られた情報ではない(改ざんされている)」ことが検出できます。このようにして、「受け取ったデータ(本文)が、原本と同じか、改ざんされているか」を識別する仕組みが作れます。ちょうど文書に「判子」や「サイン」を付けて「確かに、特定の作成者が作った文書である」ことを証明するのと同じ機能ですね。このような仕組みのデータ「本文+秘密鍵で暗号化されたハッシュ値」で署名(証明)することを「デジタル署名(デジタル証明・電子証明)」と呼び、秘密鍵で暗号化されたハッシュ値を「デジタル証明書・電子証明書」と呼びます。
なお、「デジタル証明書」の機能を簡便にカード化したものが「(非接触)ICカード」であり、現在、クレジットカードやキャッシュカード、運転免許書、(本学の)学生証などにも使われています。なお、「非接触ICカード」は、登録された情報の管理だけでなく、これらの認証のための計算や、暗号化のための計算も行う超小型の(1mm位の大きさの)コンピュータです。また、非接触ICカード(ICタグ)等は、信号の交換(入出力)だけでなく、電源も外部から「電磁波」の形で供給を受けて動作しますので、ICカード自体には電池は入っていません。なお、非接触ICカードは、殆どの携帯電話(ガラ携)・スマートフォン等にも搭載されています(NFC)。この技術を使い「クレジットカードやキャッシュカードや学生証」に(デジタルデータとして)記載されている内容が正当であることの証明しています。
また、言葉の注意として「日本の法律用語」としての「電子署名」は、ここで述べた「デジタル署名(電子署名)」とは別の意味で使われることもありますので、注意してください。偽造や改ざんに対しての(ここで説明したような)十分な技術的な配慮がされていない、たとえば「手書き文字のデータを単にビットマップとして保存したもの(タブレットに手書きでサインしてもらい、それを保存したもの)」なども、日本の法律では「電子署名」と言います(^^; 荷物の受け取りなどで「(実質的な意味の無い)判子」の代わりに「(実質的な意味のない)タブレットへの手書きサイン」が流行るところが、如何にも「日本らしい、時代遅れのデジタル化」ですね(^^;;;
ところで、Webなどで暗号化通信(TLS)を行う場合やデジタル証明等を使う場合に使う、「Webページ等で公開されていたり、メール受け取る公開鍵が正当なものか?」言い換えると「Webページやメールが偽装されていないか?」などを、どう確認すれば良いのでしょう?公開鍵が正しく受信者に届けば確かにこの方法だけで証明ができますが、公開鍵を公開しているWebサイトごと、全部偽装されたら、この方法だけでは見破れません。そこで「公開鍵が正しいかどうかを証明する、第三者機関(サイト):認証局(Certificate Authority: CA)」が使われます。認証局(CA)は、「ある人(サイト等)が発行する公開鍵が、正当なものである」ことを証明する、デジタル証明書を発行します。信頼できるサイトは、信頼できる認証局の証明を受けたデジタル証明書を発行し、その証明書によって、文書やサイトの内容が正当であることを、利用者に対して証明します。つまり、サイトのデジタル証明書があっても、その証明書が「認証局によって、正当なものと証明されていない場合には、改ざんがあるかもしれない(信頼できない)」という判断を行うことができるようになっています。では、認証局(CA)自体が偽装されたら? そこで、他の認証局が、その認証局の正当性をデジタル証明します。ではその認証局が... と、突き詰めたらきりがありません(^^;; そこで、実際には、いくつか「社会的に、信頼できるCA(ルート認証局)」があり(社会的に信頼できる企業や機関など)、そこが、他のCAが信頼できるかどうかを、証明(そのCAへが信頼できることを示すデジタル証明書を発行)しています。そして、Webブラウザなどは「信頼できる、ルートCA」をあらかじめ登録しておき(Webブラウザのインストール時に、ブラウザのメーカーが信頼できると認定する認証局を、初期値として組み込んでいます)、ブラウザに登録してある「信頼できる認証局」によって、アクセスしたサイトのデジタル証明書が信頼できるかどうか、判断しています。ですから(自分の判断では)信頼できるサイトが登録されていないこともたまにあり、その場合には、Webブラウザに「信頼できる認証局の追加」を行う必要があるかもしれません。しかし、この追加は「十分な知識と技術を持った人が、注意深く確認をしながら行う必要」があり、「普通の人は、認証局の追加作業は避けた方が良い」でしょう。認証局自体の偽装もありうるため「「信頼できる認証局」の設定は、自分で勝手にいじらない」もし「信頼できる認証局」に追加が必要ば場合には(そのようなメッセージが表示された場合には)、必ず「業務用システムについても、ネットワークセキュリティについても、本当に詳しい人)」に相談すると良いでしょう。その上で、秘匿性が高い情報を入力する場合には「暗号化通信が行われている(https://)となっている」ことを確認すると良いでしょう。なお、現在これ以上のセキュリティ技術は無いので、これが「破れない、という仮定」の上に、現在の(ネット)社会が構築されていることを、知っておくと良いでしょう。
原理的な話をしてきましたので、それを踏まえて「インターネット(特にWeb)上で実際に使われている暗号化通信技術」を紹介します。それが、SSLあるいはTLSと呼ばれる通信方法です。実際の手続きはやや複雑ですが、簡単にイメージだけ言えば
1) Webサーバに暗号化通信(https:)が要求されると、相手(クライアント)に「公開暗号鍵」とその公開暗号鍵が「正当なものであるというデジタル証明書」を伝えます。
2) そのページにアクセスしたWebブラウザ(クライアント)は、サーバーからのデジタル証明書が正当であることを確認した上で、「これから使う、公開暗号鍵方式のパスワードを、乱数などで自動発生し」それを、受け取った公開暗号鍵を用いた暗号化で、サーバーに送ります。
3) Webサーバーは、利用者(Webクライアント)から送られてきた「パスワード」を秘密鍵で復号し「承認」し、そのパスワードを使って「共通暗号キー方式」でデータを送ります。
という方法です。最初のパスワード交換だけ「公開暗号鍵方式(暗号文を作るための鍵だけ公開)」を使い、その後は共通暗号鍵方式(パスワードは一切非公開)で、しかも、その後も、自動的に短時間でどんどんパスワードを変更していきます。このような方式をとることにより、「最初のパスワードのやり取りだけ」にしか純粋な公開暗号鍵方式が使われない(すぐにパスワードが変わってしまう)ので、「その瞬間(1秒以下の、ごく短い時間)」に(スーパーコンピュータでも天文学的な時間のかかる)素因数分解の問題が解かれなければ、パスワードは破れなくなります。これは、現代の技術では「事実上、ほぼ不可能」と言っても良いくらいの困難さでしょう(逆にいえば、ほぼ不可能に近いだけであり、絶対に不可能とは言い切れません)。
現在インターネットで「セキュアな通信」と呼ばれるものは、この方式を採用しています。細かいところでの実装は何種類かあり、初期のものは「SSL(Secure Sockets Layer)」と呼ばれていますが、実装にセキュリティホールが見つかったため、現在では「TLS(Transport Layer Security)」と呼ばれるものが使われています。細かい点を除けば同じようなものですので「SSL/TLS」と一緒に呼ばれることもありますが、これがインターネット上の暗号化通信では最もよく使われる方法です(そして、最も強固です)。このような「暗号化通信」をするときは、URLは、「http:// .....」ではなく「http s:// .....」となりますので、「暗号化通信が必要な場面(パスワード入力、クレジットカード番号入力、その他秘匿性の高い情報入力)」の場合には「https:// .....」と「sがついているかどうか」を注意しましょう。また、最近のブラウザでは「暗号化通信していない場合には警告が表示される」ものもあります。
なお、現在のデジタル技術では「絶対に破れない暗号」は存在せず、「破ることが極めて困難な暗号化技術」しかないことは、肝に銘じておく方がよさそうです。
おまけ:既に、量子コンピュータを使って高速に素因数分解を行う方法(ショアのアルゴリズム)が知られており、もし将来、本格的に動く量子コンピュータが開発されれば、RSA暗号は短時間で解け、TLSなどの(素因数分解を元にした)暗号化は、近いうちに破れるかも知れません。なお、現在研究中の量子コンピュータはまだまだ不十分なもので、この計算をできるレベルの量子コンピュータはまだ存在しませんが、いずれ開発されるでしょう。そのため、素因数分解に替わる「逆解きが難しい問題」として「格子問題」の研究が行われています。これはスーパーコンピュータでも量子コンピュータでも多分現実的な時間で解くことができない問題になると期待されており、格子問題を使った「(強固な)公開暗号キー方式の暗号」が、近い将来、現実化するかも知れません。また「盗聴不可能な通信経路」を作る方法として「量子暗号通信」の研究も進んでおり、既に試作機も完成しています。これは量子力学で記述される「自然法則」により「絶対に盗聴が不可能」ということが保証されます。ただし... 実装に穴が無く完全であれば... ですが。興味のある方は、Webで調べてみてください。
このように、「公開暗号キーの技法(RSA)」と「ハッシュの技法」をうまく組み合わせると、「本文が正しいことを、(秘密鍵を所有する人が)証明する」ことができます(デジタル証明)。この仕組みを組み合わせると、「一連の情報が、お互いが、お互いの正しさを相互に証明する、という仕組み」ができます。その中の1つが「ブロックチェーン」と言われる仕組みです。ある情報の集まりを「ブロック」と呼ばれる塊にまとめます。このブロックの中身が改ざんを防止するためにこのブロックの「ハッシュ」を求めます。同質の別の情報を付け加えたいとき、「既にあるブロックに繋がれるブロック」として位置づけていきます。このとき「前の(親の)ブロックのハッシュ値を自分のブロック内にも1つのデータとして記録」していきます。
[ ブロック1 (現ブロックで管理する様々なデータの集まり、ブロック2へのリンク情報 ] -->このように、「前ブロックのハッシュ値を、次のブロック内に格納していく」ことにより、「ブロックの繋がり=ブロックチェーン」ができあがります。このように繋がれたデータは「一部を改変すると、そのブロックのハッシュと、次のブロックに格納されているハッシュ値が一致しなくなる」ため、「改ざんを、容易に発見できる」仕組みのデータになります。また、正当にブロックを付け加えるには「前ブロックから新しいブルックにチェーンを繋ぐ必要がありますから」勝手に繋ぐことはできず「正当性を確認し、正当性が確保されたときに、ブロックの追加が可能」なようにします。また、個々のブロックの中の情報は、それぞれのブロックの管理者のみが変更し、そうするとハッシュ値が変わりますから、ブロック全体のそれぞれのブロックの管理者がその変更を「承認 」して、各ブロックのハッシュ値の更新作業を終えた時点で「変更」されます。 各ブロックのデータは、同一のPC上になくても、ネットワークで(P2Pモデルで)繋がれていても構いませんので、ブロックチェーン全体のデータは、複数のPCで、それぞれのブロックの(複数の)管理者で、「分散して管理されている状態」になります。このような「分散型の、強固なセキュリティのデータベース」を「ブロックチェーン」と言います。
この技術を用いて、極めて改ざんが困難な(事実上勝手に改ざんできない)データを扱うことができます。実装には様々なバリエーションがあり、例えば、「勝手に改ざんできない、誰もが閲覧できる」とか、「暗号化され、管理者以外閲覧できない、しかし暗号化されたままの複製はいくらでも作れる(バックアップが容易なため、事実上破壊できない)」とか、「強力な分散型のデータベース」として、様々な活用が試みられています。
ちなみに、ブロックチェーンの仕組みは、2008年に「(ペンネーム)Satoshi Nakamoto」により提案された一連の論文の一部であり、Satoshi Nakamoto の提案は、ブロックチェーンの手法だけでなく、新しいブロックを作る仕組みとして「ある暗号を解読した(条件にあったハッシュ値を答えとする元の数値(nance)を見つけた)ものだけが、新しいブロックを作ることができる」という仕組みを加え、その「労力」に対して「報酬(一定量のビットコイン)」が得られる仕組みを作り、さらに、そのブロックの所有者は、その「報酬(ビットコイン)」を所有し、その所有権を他のブロックの所有者と交換できる仕組みを加える事により、「埋蔵量は有限」であり「採掘にはそれなりのコスト」が掛かり、「交換はできるが複製はできない」という(貨幣として使われる金(きん)などの)貴金属などと同じような性質を持たせたものを作ることが可能である、と提唱しました。この仕組みを実際に実装したものが「ビットコイン」です。
ところで、ビットコインは確かに、「埋蔵量は有限」であり「交換はできるが複製はできない」という性質を持っています。が、「金(きん)は、それだけで金属としての利用価値があります」が、ビットコインは、これだけでは全く利用価値がありません。ところで「紙幣」というのも「只の印刷された紙きれ」ですからそれだけでは全く利用価値がありませんが「商品や他の国の貨幣等と交換できる」ために「貨幣価値」を持ちます。そこで、ビットコインなども「通常の貨幣で売り買いする仕組み(取引所)」を加えると、一種の貨幣としてふるまうことが期待されます。このようなものを現在では「暗号資産」と呼んでいます。なお、暗号資産は、古くは仮想通貨と呼んでいた時代もありました。
現在、「暗号資産」と呼ばれているものは、そういう仕組みのものです。なお、紙幣と同じくビットコイン自体に価値があるわけではありません。ある国の紙幣は、国が破綻すると只の紙くず(おもちゃの「こども銀行券」とおなじ)になりますが、ビットコインも同じで「誰も買わなければ、只のゴミ」になります。このような振る舞いもまた、普通の「通貨」と同じです。
また、ブロックチェーンの形で「デジタルデータと、その所有権者」の情報管理すると、(デジタルデータ自体は容易に複製可能ですが)その正規の所有権者を管理することが可能になります。これをNFT(Non-Fungible Token)と呼ぶことがあります。仮想通貨のブロックチェーンと似ていますが「交換も複製もできない」ように管理します。これも「通常の通貨や、暗号資産等で売買できるような仕組み」を加えると、たとえば「デジタル化された美術品」等の製作者や所有者管理や、所有権の売買が可能になります。既に「ゲーム」等で、獲得したアイテムやポイントなどをNFTに格納して他のゲームで使ったり、(ゲーム管理会社とは別組織で)売買できるようにしたものなどもありますので(NFTゲーム)、ゲームの課金ビジネスもいろいろ変わっていくのかもしれません。
なお、ここで気を付けておくべきことは「通常の絵(アナログ)等の鑑定による製作者の特定(および複製された偽物の発見)」と同じレベルのことが、デジタル技術でも、ブロックチェーン技術等の活用により可能になっただけ、ということです。NFTで売買されているかどうかと「元のデータに価値があるかどうか」とは無関係です。また暗号資産も「紙幣(アナログ)」と同じレベルのことが、デジタル技術でもできるようになっただけのことであり、「その暗号資産に価値があるかどうか」とは無関係です。どちらも「欲しい人がいれば高く売れ、欲しい人がいなければ単なるゴミ」です。これは「絵画や、紙幣や株券、さらにはおもちゃの「こども銀行券」なども同じ性質を持つ」ものですが、「国家とか、有名鑑定師等のお墨付きがあれば、価値があるものと誤解している」人も多いかもしれませんね。国や鑑定士が価値を決めるのではなく「市場(買いたいと思う人)」が価値を決めるというのが市場経済の原理です。なお、ある国の「紙幣」がどの程度信用できるのか? は、それを保証する「国」の信用度によります、なお国は「いくらでも」紙幣を印刷して発行できますので、その権利を乱用したりするとその国の通貨は暴落し、その国の経済は破綻します。また、その国の印刷技術が稚拙であれば、紙幣は偽造され、やはり信用を失い通貨は暴落します(^^;)先進国なら高い印刷技術を持ちますが、それほど印刷技術が高く無い国などの場合には、低い技術で印刷された(簡単に偽造できる)紙幣などより「暗号通貨の方が偽造が困難でしかも発行数が有限であることから、信用できる」という場合もあるかもしれません。実際「暗号資産を法定通貨にする」国も、いくつか現れ始めているようです。なお、原理的には破ることが極めて困難な方式でも、その実装や運用(特に、管理システムの管理とか、管理パスワード管理など)に穴があれば、意外と簡単に破れてしまうことがあることも、意識しておくと良いと思いますし、実際に大量の暗号資産の盗難事件などが起きています。
まず最初に、皆さんが既に使っている「アカウントのパスワード」の管理方法と「パスワードのつけ方」の話から始めましょう。
【大学アカウントとパスワード】
演習室のPCから、大学アカウントのパスワード変更:
https://www.kppuc.ac.jp/webmtn/LoginServlet
今までのアカウント名とパスワードでログインし、新しいパスワードを2回入力してください。なおパスワードは9桁以内が保証されています。
なお、パスワードの変更は、大学アカウントにかかわるすべての操作に影響を与えますので、「最初に」変更するか、あるいは「全ての場所のパスワードが変わる」ことを念頭に置いて、おちついて行います。
では、設定する「パスワード」はどのように作ればよいのでしょう?
パスワードが破られると、他人から「本人になりすまし」され、場合によっては自分の財産(お金だけでなく、社会的信用とか友人関係、自分の権限)を盗まれることもあります。ですから「パスワード」は「盗まれないように注意する」必要がありますが....「注意して!」と抽象的に漠然と言うのは簡単ですが、「具体的に、どうしたらいいのか」わかりますか???
まず「破りにくく覚えやすいパスワードを幾つでも簡単に作れる能力が無い人」の場合、どのような問題があるのかを、簡単に説明します。
直ぐに破れるパスワード簡単なパスワードの利用は論外としても、大抵の方は、時間を掛けてじっくりと考えれば「「幾つでも」とはいかないにしても、1つくらいなら」やぶりにくいパスワードを作れる方が多いのではないかと思います。
ところで、「パスワードを使いまわすな」とか「定期的にパスワードを変えろ」とか言われ、「その意味する内容や理由を知らずに、単に『しつけ』として、そのような指示に盲目的に従っている」人も多いかもしれません。しかしこれは「大抵の人は、やってはいけないこと」なのです。
大抵の人(=破りにくく覚えやすいパスワードを幾つでも簡単に作れる能力が無い人)の場合、「パスワードを変えろ」とか「別のパスワードを使え」と言われたら、次にどのようなパスワードを作るでしょうか? 最初は気合を入れて破りにくいパスワードをつけるかもしれませんが、考えるが面倒なので、次第に「以前より簡単なパスワード」を作る傾向になることが知られています。そのため、頻繁に変えれば変えるほど「より、セキュリティの低いパスワード」に移行し、最後には「簡単に破れるパスワード」に移行することが多いようです。
ですから今は、大抵の「破りにくく覚えやすいパスワードを幾つでも簡単に作れる能力が無い人」には「パスワードは頻繁に変えるな(定期的に変えるのはもってのほか)」「全て認証で異なるパスワードを使うのではなく、数種類の(覚えられる程度の)強固なパスワードを、セキュリティの必要性を勘案し、使い分けあるいは使いまわししろ」とアドバイスすることが「現代的」となっていますし、実際、その方が圧倒的にセキュリティは高くなります。また、現在では「パスワード変更操作」を偽装してパスワードを盗む(偽装サイトの手法)も多く見られますので「パスワードを変更すること自体が1つのリスク」と捉えることも重要です。
# パスワードは定期的にとか、変えてくださいと言われて変えるものではありません。今までのパスワードのセキュリティに疑問を感じた時に「自らの判断よって、自主的に」変えるものです。
今までのパスワードにセキュリティ上の問題があると感じた時、あるいは複数の場面での認証に独立性を持たせセキュリティを確保したい時、「新しいパスワードを作る」作業が必要ですし、セキュリティ確保が重要になればなるほど、その機会が増えていきます。そのとき「破りにくく覚えやすいパスワードを、幾つでも簡単に作れる能力」が必要になります。
登録したパスワードは、そのまま(平文)ではなく「ハッシュ値」で保存されています。ところで、「公式などの簡単な計算で A→B は簡単に解けるのに、B→A を求める公式が存在しない」場合(一方向性関数で変換したハッシュ値を使う場合)、この問題は本当に「解けない」(ハッシュ値から、パスワードを求めることはできない)と言い切れるでしょうか? 実は、このような問題は公式では解けませんが、「試行錯誤」による方法で、十分な手間を掛ければ解くことが可能です。
問題を具体的に、「ダイヤルロック(自転車などに付ける、暗証番号方式の錠)」の破り方を例にして、説明します。
まずダイヤルロックのダイヤルを「ある適当な番号」にセットし、ロックが開くかどうか、確かめます。
もし「開けば正解」とわかるし、「開かないなら、その番号ではない(正解はそれ以外の番号である)」ことがわかります。 パスワードの問題では、「ある適当な文字列」に対するハッシュ値が「パスワードファイルに存在するなら正解」とわかり、「パスワードファイルに存在しない」なら正解パスワードはその文字列ではない(それ以外の文字列である)、ことがわかることに、相当します。
ダイヤルロックもパスワードも、「ある適当な番号(適当な文字列)」で試すのが1回だけなら、かなり運が良くなければ開きません(ある程度セキュリティが保たれます)。しかし「何回でも繰り返せる」場合には、事情が一変します。
3桁のダイヤルロックなら、各桁、0から9までの全ての場合を順に試せば「1000回以下の試行」で、必ず破れます。4桁のダイヤルロックでも1万回以下の試行で必ず破れます。人間が1つずつ手で試行する場合には1万回の試行は「とても面倒」です。しかし、コンピュータを利用する場合には、皆さんのスマホでさえ「1秒間に10億回以上の計算を行う能力」がありますから...(^^;
このように、全ての可能性を虱潰しにチェックしていくパスワードの破り方を「総当たり法」と言います。1桁に入る可能性は、数字なら0~9の10通りですが文字などが含まれる可能性あれば数十通りになります( \( a \) 通りとおきます)。また桁数を \( n \) とすると、 その組み合わせの数(つまり破るのに必要な試行の回数)は\( a^n \)通りとなります。\( a \) や \( n \) を大きくすると\( a^n \)は飛躍的に大きくなりますから、絶対に破れないわけではないが「現存する世界最高速のスーパーコンピュータでも、確実に破るには、数千年以上かかるくらい面倒」にすることも、比較的容易におこなえます。
つまり総当たり法で破りにくいパスワードは「それぞれの桁に何が来るかわかrない、できるだけ長い文字列」となります。
ところで皆さんはパスワードに使うような「長くて複雑な文字列」を覚えられますか? 覚えられなくて何処かにメモすると「そのメモを見られたら」一瞬でパスワードは破られます(パスワードを機械に記録するのも、同じ危険性を持ちます)。
ではどうしたら良いでしょう?
よく行われる悪い方法は「意味のある文字列=単語」およびその組み合わせを使う方法です。これなら覚えやすいです(「悪いパスワード」や「最悪のパスワード」等のキーワードでWeb検索してみてください)。
そこでパスワードを破る人たちは「全ての単語を含む辞書」を作り、「辞書に含まれる単語(文字列)、及その組み合わせ」を候補として、パスワードを破る仕組みを開発しました。全ての単語とその組み合わせというと膨大な量と思いがちですが、全ての文字の組み合わせの数から比べると、ほんのわずかな個数(数十億とか数百兆とか)になります。試しに出鱈目にキーボードを打って、偶然「単語」が打たれることがどのくらいか、感じてみてください。つまり「長いパスワード」でもこれが「既存の単語、あるいはその組み合わせ」だと仮定すると、それほど「場合の数」が多くはないので、高速なコンピュータなら現実的な時間で、パスワードを破ることができます。この破りを「辞書法」と言います。
辞書法で破られないためには「辞書」に乗っている単語の組み合わせは避けることが必要になります。そしてこの「辞書」には、日常使われる単語だけでなく「ネット上の文書に現れる単語」や「過去に破られたパスワード」なども乗っています。 では「辞書法でも、総当たり法でも、簡単には破られず、しかも覚えやすいパスワード」はどのように作れば良いでしょうか?
破ることが可能でも「破るのがとても面倒」であれば「錠」として十分実用的になります。実際「破るのは極めて難しく面倒で、手間がかかる錠」はありますが「(どんなプロの手に掛かっても)破ることが不可能な錠」は多分存在しません。実際、家庭用の錠などは「鍵をなくして困ったときに、専門の鍵屋さんにお願いすると」いとも簡単に開けてくれます(^^;
それでも錠として機能するのは、一般の人にとっては破るのが「とても面倒」だからです。その面倒さに見合う利益(価値)がなければ、たとえ犯罪者でもその錠を破ろうとは思いません。ましてや「隣に、鍵が掛かっていない(空きセキュリティがら空きの)家」があるなら、なおさらです。錠の場合と同じ理由で「絶対に破れないパスワードは存在しません」が、破ることが極めて困難なパスワードであれば、十分に機能します。パスワードによりセキュリティを守る上で大切なことは、パスワードファイル(ハッシュ)が盗まれても、そこから「自分のパスワードを破るには手間が掛かる(他の人のパスワードを破る方が楽)」という状態に持っていくことです。
まず最初に断りますが「ここで紹介するのは1つの例」であり、これを参考にするにしても「必ず、自分流に、変えて」作ってください。
まず、パスワードそのものを覚えるのではなく、覚えやすい「パスワードの元」を準備します。これは「なるべく長い、複数単語からなる、覚えやすい文」から出発します。例として、あまり適切でない例(あまり長くないベタな文字列)として、
パスワード元:KAZAMA HIROSHI
から出発してみましょう。原理や威力を知るためです。元は「辞書にある2単語」ですから、このままでは、辞書法で瞬殺されます。これを「自分が暗記暗算できる程度の簡単な変換ルール」で変形します。たとえば「単語の最初4文字」を切り出します。
KAZA HIRO
次に「最初だけ大文字」にします。
Kaza Hiro
次に「空白は&に」「2回目のaは@に」「iは1に」置き換えます。まあ、一昔前の「ギャル文字」のような感覚です。すると、
Kaz@&H1r0
という文字列になり、多分「辞書法」では破れず、「総当たり法」でも破りにくい比較的強固なパスワードになります。
この方法のポイントは
1)「単語のある部分を切り出してつなげる」という操作により、辞書法で破れない「辞書にない文字列」を生成する
2) 「置き換え」により「大文字、小文字、数字、特殊記号」を混在させ「総当たり法で破りにくくする」
ことです。方法はいろいろありますので、「覚えやすく、暗算でできる、自分なりの変換ルール」を各自考えてみてください。
たとえば、「各単語の最初の1文字」(大文字小文字特殊記号はそのまま)という単純なルールでも、
パスワードの元:To be, or not to be: that is the question に対して
Tb,ontb:titq.
となります。1つくらい数字が欲しい気もしますが. これだけでも結構強固なパスワードになります。数字を加えたければ、例えば「o[オウ] →0[ゼロ] に変換」を加えれば
Tb,0ntb:titq.
となり、かなり強固なパスワードになります。この例の場合、覚えるのはパスワード(Tb,0ntb:titq.)ではなく「パスワードの元」となる文章「To be, or not to be: that is the question.」と「変換ルール」「各単語の最初の1文字切り出し(記号はそのまま)、アルファベットのオウ(o)は数字のセロ(0)に置き換える。」です。なお、「変換ルール」に従った変換はパスワード入力時に「暗算で」行います。
「自分の変換ルール」が漏れなければ、同じ変換ルールをいつまでも使い使い続けることができ、「パスワードの元」さえ変えれば「覚えやすくて破りにくい」パスワードをいくらでも量産できます。また、「自分の変換ルール」さえ極秘(自分の頭の中だけ。他人に言わないしメモも残さない)にしておければ、「パスワードの元」の管理が多少雑でも、パスワード自体が漏れる可能性は極めて低くなります。今回の授業内容で「ハッシュ」を学んだ皆さんなら、この手法は「人力 ハッシュ」とでも言うような手法(自分の変換ルール=一方向性関数=ハッシュ関数)であることに気が付くかもしれません(^^)
他にも様々な作り方がありますので、興味のある方は、Webで「パスワードの作り方」をいろいろ調べてください。たとえば、総当たり法に対する防衛は、多様な文字種を用いる方向もありますが「単純に桁数(文字数)を増やす」方向も有効です。
そして、今日学んだパスワードの破り方「総当たり法」と「辞書法」のどちらでも「極めて破りにくいパスワードかどうか」検討してください。また、「自分が作ったパスワード候補」がどのくらい破りにくいかを判定するサイトもありますので、興味のある方は探してみてください。ただし「量産品のうち使わないゴミ」をテストするだけに留め、「本物のパスワードは絶対に入力しない」よう、気をつけてください。
皆さん「自分なりのパスワード作り方(変換ルール)」を、1つだけで良いので、じっくりとよく考えて編み出してください(時間外学習でかまいません)。そして「その作り方(変換ルール)は、誰にも言わない自分だけの秘密」にしてください。それは皆さんの「これから先、一生使える財産」になります。
パスワードは、漏れないように注意。「暗号文」と「パスワード」は同じ通信経路は使わない(「パスワードは別メールで...」は、セキュリティ意識の低い日本の役所発祥の無意味な習慣。メールが盗聴されていれば、別メールであろうと同じように盗聴されているので、パスワードの意味がなく、他のセキュリティ確保の方法も無効化されるため、現在は「PPAP使用禁止」が望ましいです。(キーワード「PPAP全面禁止」「PPAP問題」等で検索してみてください。「ピコ太郎 PPAP 全面禁止」で検索しても面白いかも(^^; )。
パスワードは、必ず「別経路」で送るようにしましょう。直接、電話、Fax、などの方法がよく使われます。また、「業務用メールと個人携帯電話の紐付け情報が漏れていなければ」業務用メールで暗号化されたデータ、携帯電話のメールでパスワード、という方法もありえます。2段階認証とか、スマホで認証と言う方法が、これにあたります。
では、今日は、このへんで終わりにします。