では、中心極限定理(実際にはその上位互換)を使って、サンプルデータを元に「母集団の平均値\(\mu\)」について考察してみましょう。
実際には「母集団の性質(平均値や標準偏差)」を調べることが困難だから「サンプル」を取るのですが、まずはその「原理」を知る(イメージする)ために、「母集団の性質が分かっている場合(正解が分かっている場合)」から、説明を始めます。
まず中心極限定理を復習します。(テキストでは、サンプル内のデータの平均を \(\bar{X}\) と書いていますが、いくつもの異なる平均操作や、いくつもの異なる平均値や、平均値の分布も出てきますので、まずそれを整理しておきます)。
母集団の平均値:母平均\(\mu\) (本当は、求めるべき答え)
母集団の分散値:母分散\(\sigma^2\)
母集団の標準偏差:母標準偏差\(\sigma\)
ここから「\(n\)個」データをとります(ランダムな復元抽出)。これをサンプル(標本)と呼びます。とった\(n\)個のデータを、ここでは{\( x_i:i=0,1,...,n\) }、テキストでは\(X\)と表しています。
サンプルの大きさ:\( n \)
\( n \)個の平均をとります。これをサンプル平均(標本平均)と呼びます。ここでは \( Y \) , テキストでは\( \bar{X} \)と書いています。なおテキストの\(\bar{X}\)を\(Y\)と書いたのは、後でこれを「変数」として扱うからです。「変数」は簡単な文字で表した方が、皆さんイメージしやすいだろう、という配慮です。
サンプル平均:\( Y= \frac{1}{n}\sum_{i=1}^{n} x_i =\bar{X} \)
「サンプルを取り、サンプル内のデータの平均を求める」ことを「1回の事象」のように扱います。
\( N \) 回この事象(大きさ \( n \)のサンプルを母集団から抽出し、その値の平均値を求める)を繰り返えした時、\(k\)回目のサンプル平均を、\(Y_k\)と書きましょう(テキストに準拠した記号で書くとすれば、\(\bar{X}_k \) とでも書くべきものです。ただしこの記号はテキストでは使っていませんので\(E( \bar{X})\)の意味がわかりにくくなっています )。\(N\)個の(サンプル平均値)データの集まりを、ここでは{\(Y_i:i=0,1,...N\) }と表しましょう。テキストではこの平均値の集まり「も」\(\bar{X}\)と表しています。
この先、{\(Y_i:i=0,1,...N\) }を「注目する『データ』」として扱い、その『データ』の「頻度分布」やそれと比例する「確率分布(起こる回数の比率)」などを検討していきます。サンプルのデータではなく「サンプル平均を1つのデータとして扱う」ところが、混乱しやすいところです。
このとき「確率変数\( Y \)(サンプル平均)の確率分布は、正規分布\( N(\mu,\sigma^2/n )\)になる」というのが、中心極限定理です。つまりサンプル平均の値が「\( Y \)くらいの確率\(P(Y)\)」は、
\[ dP(Y) = N(\mu,\sigma^2/n ) dY=\frac{1}{\sqrt{2 \pi } {\sigma/\sqrt{n}} } e^{-\frac{(Y-\mu )^2 }{ 2 \sigma^2/n }} dY = \frac{1}{\sqrt{2 \pi } {\sigma/\sqrt n} } \exp{ \left( -\frac{(Y-\mu )^2 }{ 2 \sigma^2/n } \right)} dY \] となる、という意味です。
ここで、「\(N\)回の事象の平均」を取ることを\(E(□)\)という記号で表すことにすれば、そのようにして得た「サンプル平均値の、事象間の平均\(E(Y)\)」は、
サンプル平均値の平均:\( E(Y)= \frac{1}{N}\sum_{k=1}^{N} Y_k =\frac{1}{N}\sum_{k=1}^{N} {\bar X}_k = E(\bar{X}) \)
となります。 後ろの2つは、テキストを参考にする時に対応がわかるよう「テキストの記号に準拠した」記号で書いたものです。「平均値の平均」... 「何の?」が曖昧だと、ここで全く意味がわからなくなります。「サンプル内での\(n\)個の平均」をとるときの足を\(i\), 「\(N\)回繰り返したときの、サンプル間での、平均」を取るときの足を\(k\)と、記号を分けて書きました。
この2種類の「平均」の意味の違い(区別)を正確に把握してください(先に進む前に、必要があれば、落ち着いてここまで何回も読み返してください)。
すると、前に2項分布で「コインが \( x\) 枚くらい表になる確率」を議論しましたが、全く同じ仕組みで「サンプル平均が \( Y \) くらいになる確率」を議論することができます。「サンプル平均」という量が(平均という名前はついているけど)、1つの事象(コインを振ってx枚表が出た)に対応する「1つの量(確率変数)」であることを、抑えてください。
ではもう一つ、コイン投げやアンケートの話も「復習」しておきましょう。
10枚のコインを投げ、x枚表になる確率は、
x B(x,10,1/2)
0 0.001 = 0.1%
1 0.010 = 1.0%
2 0.044 = 4.4%
3 0.117 =11.7%
4 0.205 =20.5%
5 0.246 =24.6%
6 0.205 =20.5%
7 0.117 =11.7%
8 0.044 = 4.4%
9 0.010 = 1.0%
10 0.001 = 0.1%
でした(合計1=100%です)。
このとき、平均値(期待値)は5枚です。しかし5枚ちょうどになる確率はわずか25%くらいしかありません。では「5枚くらい」を「3?7枚」とみてみましょう。すると「5枚くらい」の確率は89%くらいになります。つまり「9割くらいの確率で5枚くらい(3から7)枚になる」と言えます。もし「表の枚数が5枚くらいで無い(0か1か2か8か9か10枚)ことが起これば」それは「およそ10%くらいの確率のこと」が起こったと言えます。この確率の値をp-valueと呼びました。「くらい」の範囲を変えながらこのp-valueをみていきます。
| 範囲 | 範囲内の確率 | 範囲外の確率(p-value) |
|---|---|---|
| 5 | 25% | 5%=0.75 |
| 4-6 | 66% | 34%=0.34 |
| 3-7 | 89% | 11%=0.11 |
| 2-8 | 98% | 2%=0.02 |
| 1-9 | 99.8% | 0.2%=0.002 |
| 0-10 | 100% | 0%=0 |
もし「11枚表」なら... 「それはあり得ない」と判断するでしょう(^^;。全部で10枚なのですから。表で言えば、11枚は、0-10枚の範囲外ですから、これはp-value=0。つまり「そういうことが起こる確率は0」とも言えます。もしそれが起これば「何か前提と違う」と結論できます。
もし「10枚表」なら... 10枚は、1-9枚の範囲外ですから、これはp-value=0.002。つまり「そういうことが起こる確率は0.2%」とも言えます。絶対に起こらないとは言えませんが「かなり稀なこと」です。そのような稀なことが「偶然、運よく起こった」可能性もありますが「何が前提が違う(例えば表が出る確率が1/2では無いのでは?)」という可能性もありそうに思います。もし「偶然、運よく起こることがある」と解釈する基準を1%までとするなら、それより確率が小さいので、これは「偶然では無いだろう」と判断することになります。このような「偶然、起こることがあると判断」するか「起こらないと判断」するかの基準を「有意水準」と呼ぶことがあります。この言葉を使えば、このことは、有意水準1%で「偶然に起こったとは考えにくい(=偶然でない「何か」があるかもしれない)」という判断になります。
もし「9枚表」なら... 9枚は、2-8枚の範囲外ですから、これはp-value=0.02。つまり「そういうことが起こる確率は2%」とも言えます。絶対に起こらないとは言えませんが「そこそこ稀なこと」です。そのような稀なことが「偶然、運よく起こった」可能性もありますが「何が前提が違う(例えば表が出る確率が1/2では無いのでは?)」という可能性もありそうに思います。もし有意水準1%で判断するなら「2%の確率のことが偶然起こった」と判断します。もし有意水準5%で判断するなら「5%以下の確率のことが起こったとは考えにくい(=偶然では無い「何か」があるかもしれない)」という判断になります。
もし「8枚表」なら... 8枚は、3-7枚の範囲外ですから、これはp-value=0.11。つまり「そういうことが起こる確率は11%」とも言えます。あまり起こらないとも言えませんが「まあまあ稀なこと」です。そのような稀なことが「偶然、運よく起こった」可能性もありますが「何が前提が違う(例えば表が出る確率が1/2では無いのでは?)」という可能性もありそうに思います。もし有意水準1%や5%や10%で判断するなら「11%の確率のことが偶然起こった」と判断します。もし有意水準20%で判断するなら「11%の確率のことが起こったとは考えにくい(=偶然では無い「何か」があるかもしれない)」という判断になります。ただし、このへんになると「確率20%未満のことが起こったとは考えにくいという判断基準は、甘すぎないかい?(^^;」と普通は言われるでしょう。
もし「7枚表」なら... 7枚は、4-6枚の範囲外ですから、これはp-value=0.34。つまり「そういうことが起こる確率は34%」とも言えます。あまり起こらない... いや、確率1/3くらいだから「普通に起こる」ことでしょ(^^; ジャンケンで勝つ確率と同じですし。もちろん有意水準40%で「確率40%未満のことは起こらないと判断する」という「でたらめな判断」をするならそれを否定はしませんが... 普通は無視されるでしょう(^^;
もし「6枚表」なら... もし「5枚表」なら... 当たり前に起こることですから、省略します。
次に、「これと全く同じこと」を、(表の枚数の代わりに)サンプル平均で行います。
では最初に、「(分かっている)母集団から10個のデータを取り、平均値を求める」ということをやってみましょう。この値を \( Y \) とします。
最初の例題として「0~10の一様分布」を考えます。平均値(期待値)\(\mu\)は5、分散は\( \sigma^2=10^2/12=8.333\)くらい、標準偏差は \( \sigma=2.887\) くらいになります。
この場合、1つ取った時の値は「0~10の間の数」であり、どの数が出る確率(密度)も一定です。
たとえば10個取ると、( 6.122, 9.102, 2.275, 9.315, 7.262, 4.283, 2.977, 1.290, 5.771 7.583) となり、その平均値(標本平均)は 5.598です。1回目のサンプリングで得られた標本平均が5.598 なので、これを\(Y_1\)= 5.598 と書きましょう。
同じことを、また行います。得られた10個のデータは、( 5.831, 3.152, 5.384, 4.920, 7.737, 4.497, 9.923, 4.621, 6.221, 4.700) でした。この平均値(標本平均)は 5.699 です。2回目の標本平均を、\(Y_2\)= 5.699 と書きましょう。
同じことを、また行います。得られた10 個のデータは... 省略します(^^; この平均値(標本平均)は、3.645 でした。3回目の標本平均を、 \( Y_3 \)= 3.645 と書きましょう。
同じことを、また行います..... と、1000回、同じことを繰り返します。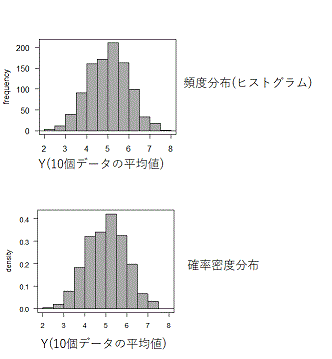
すると、(5.598, 5.699, 3.645, ....) の千個のデータ、つまりサンプル平均値のあつまり ( \(Y_i: i=1~1000 \) ))が得られます。
このデータをヒストグラムにすると、右図(上)のようになります。縦軸が「回数(頻度)」なので、これを全体の回数で割り「確率密度」で表示します(右図(下))。サンプル平均の確率分布は正規分布に近いことが確認できます。
このグラフを見ると、「サンプル平均は、5くらいのことが多い」ことがわかります。
「くらい」の範囲をどう設定するかにより、「5くらい」の頻度(確率)がかわります。
範囲の広さ(の半分)を、\( L \)と置きましょう。範囲は\(5-L ~5+L\)で表しましょう。
確率密度関数を\(f(Y)\)と置けば、「5くらい」の確率は、\(P(5-L<Y<5+L)= \int_{5-L}^{5+L}{f(Y)}dY \)です。そして、この確率密度関数が「平均値(期待値)\(\mu\)、標準偏差\( \sigma/\sqrt{n}\)の正規分布関数になる」というのが中心極限定理で、今の場合は、\( \mu=5, \sigma=2.887, n=10\)ですから、「平均値(期待値)\(\mu=5\)、標準偏差\( \sigma/\sqrt{n}= 0.913 \)の正規分布関数になる」ということを意味します(今の、1000回の試行結果は、実際に、それに近いことが、グラフから確認できます)。
これが「コイン投げの5枚くらい表がでる確率」と同じ役割をします。
では、1回(大きさ10のサンプルを取り、10個のサンプルの平均値を計算し)標本平均を求めたところ、「5」という数値が得られたとします。これは確率密度最大ですから、まあ「普通に起こること」ですね。
では、1回(大きさ10のサンプルを取り、10個のサンプルの平均値を計算し)標本平均を求めたところ、「6.1」という数値が得られたとします。これは、\( L=1 \) の5くらいの範囲\(P(4<Y<6)= \int_{5-L}^{5+L}{f(Y)}dY \)、図(グラフ)の\(Y=4~6\)の面積(0.65程度)の範囲の外ですから、このこと(5くらい、の範囲外)が起こる確率(p-value)は...0.35程度ですから、「普通に起こること」ですね。
でも、1回(大きさ10のサンプルを取り、10個のサンプルの平均値を計算し)標本平均を求めたところ、「7.1」という数値が得られたとします。これは、\(L=2\)の5くらいの範囲\(P(3<Y<7) \)、図(グラフ)の\(Y=3~7\)の範囲の外の面積ですから、このこと(5くらい、の範囲外)が起こる確率(p-value)は...グラフから見ると、0.05程度で以下すから、「あまり起こらないこと」ですね。
このような形で「そのサンプル平均が得られる確率」が(コイン投げと同じように)求められます。
なお一般に、サンプル平均 \( Y \) が、「\(\mu\)くらい(範囲±\(L\))」の確率\(P(\mu-L<Y<\mu+L ) = \int_{\mu-L}^{\mu+L}{f(Y)}dY\)は、確率密度\(f(Y)\)が平均値\(\mu\)標準偏差\(\sigma' =\sigma/\sqrt{n} \)の正規分布に従うなら(中心極限定理を認めれば)、その仮定だけから(1000回もの試行実験をしなくても)値を求めることができます。コンピュータなら「任意の \( L \) に対してその範囲外の確率(p-value)を求める」ことも、また逆に「範囲外になる確率を指定して、その範囲
\( L \) を求めること」も簡単にできます(R(EZR)なら自動的に答えが出てきます)。
この計算を、コンピュータを使うのではなく数表を使って行う場合には、例えば、「上側に範囲外になる確率」や「下側に範囲外になる確率」に対応する点(パーセント点と呼びます)の(標準正規分布表の)数表を引くと、例えば5パーセント点(対称なので95%点でも絶対値は同じ)は1.645とあるので、これに今の分布の標準偏差を掛けて、\[L=1.645 \times \sigma' = 1.645 \times \frac{\sigma}{\sqrt{n}}\]と求めます。上側に外れる時が5%下側に外れる時が5%ですから、合わせて「どちらかに外れる確率が10%」となります。つまり、「\(Y\)が\(\mu\)くらい(範囲± \( L \) )では無い確率が10%」になる範囲 \( L \) を求めることができます。なお、ここまでは、母平均や母分散(母標準偏差)が分かっている時の話ですが、実際は母分散が分からないことが普通ですから、その場合は「母分散が、サンプルの普遍分散で近似できる」という仮定の範囲内の計算をします。つまり、\[L=1.645 \times \sigma' = 1.645 \times \frac{\sigma}{\sqrt{n}}≒ 1.645 \times \frac{s}{\sqrt{n-1}}\]と近似して議論します。また、確率を10%ではなく 5%で議論したい場合には、2.5パーセント点1.96を使い、\[L=1.960 \times \sigma' = 1.960 \times \frac{\sigma}{\sqrt{n}}≒ 1.960 \times \frac{s}{\sqrt{n-1}}\]同様に1%で議論したい場合には0.5パーセント点2.576を使います。
「もし母平均がμ0だと仮定したら、今のサンプル平均値が得られる確率はどのくらいか?(p-value)」という問題は、ここで述べた計算で行います。これを「平均値の検定」と言います。
また、「今のサンプル平均が得られる確率が**%以上になる、母平均 \(\mu\)の範囲は?(**パーセント信頼区間の推定)」という問題は、母平均から見たサンプル平均のずれと、サンプル平均から見た母平均のずれは同じなので、得られたサンプル平均 \(Y \) 「くらい」の範囲が(先ほどの) \(L\) になりますから、指定された確率になる範囲Lを使い、( \(Y-L~Y+L\)) と推定できます。もし表を使って「90%以上の確率」で推定すると、
\[ (Y-L ~Y+L) = (Y-1.645 \frac{s}{\sqrt{n-1}} ~ Y+1.645 \frac{s}{\sqrt{n-1}} ) \]
の範囲となります。もし95%の確率で推定したいなら1.645のところは1.960、もし99%の確率で推定したいなら2.576を使います。これを「母平均の区間推定」と言います。
なお、数表を使うのではなく、R (EZR)を使う場合には、平均値の検定と区間推定は同時に(自動的に)やってくれます。
では次に、実際にR(EZR)を使って、母集団からランダムサンプリングを行い、得られたサンプルだけから母集団の平均値を推定してみましょう。最初に母集団を用意しますから、「問題の正解(母集団の平均値)」が分かっている問題です。これを「サンプルから求める」ことを行い、「どの程度妥当に求められるのか」をみていきましょう。「この程度妥当に求められる、この程度怪しい」という感覚が身につけば、実際の「正解がわからない問題」にも、(どの程度信用でき、その程度信用できないかを踏まえて)妥当に使うことができるでしょう。
では実際に「サンプル」から母平均を推定する方法の仕組みを見ていきましょう。実際の推定では母平均は分からない問題を扱いますが、それでは妥当に推定されているのかどうかわかりません。そこでまず、「正解が分かっている問題」を作って、実際に(R:EZRで)解いてみて、どのように推定が行われ、どの程度妥当なのかを、見ていきます。
ではまず、(演習室PCなどで)EZRを起動してください。
まず最初に、母集団が「0~10の一様分布」の場合を考察してみましょう。これは平均値(期待値)は5で、標準偏差は0.91287です。今の場合はこのように「母平均の正解」が分かっていますが、これを「知らない」としてサンプルから推定してみましょう、ということです。そこでまず、ここから10個のデータを取り、次に「その10個のデータだけを頼りに」母平均の値を検討してみます。
まず、母集団から10個のデータを取ってみます(問題作りです)。
EZR では、[標準メニュー][分布][連続分布][一様分布][一様分布からのサンプル...] を選択します。データセット名はそのまま[UniformSamples]のままで良いでしょう。もちろん名前を変えても良いですし、実際解析では、Excelから入力したデータに適当な名前を付けて使います。
最小 0
最大10
Number of samples(rows) 10
Number of observations(columns) 1
とします。これは、「0(最小)~10(最大)の一様分布で、10個のデータを、サンプルとして1回取る」という意味です。[データセットに追加する」は「何も選択しない(全部チェックを外す)」ようにしてください(データサンプルだけから推定する練習問題を作るのですから)。ここで[OK]を押すと、データ数10のサンプルが作られます。たとえば、
1.351587
9.420422
6.113978
6.868739
1.003591
8.083854
4.742664
2.314498
1.455978
6.543628
という10個のデータが、「UniformSamples」名前のデータとして生成されます(データの値は、サイコロをふるようにランダムに生成していますので、毎回違います)。Rコマンダーウィンドウのメニュー下に、
データセット[UniformSamples] [編集][表示][保存]
という表示があると思います。これはこれから解析するデータは[UniformSamples]という名前のデータだということで、もしデータを見たければ[表示]を押せば、データが見られます。
# なお、サンプルの平均値は5.713786で、普遍分散は9.427244になります。サンプルの平均値は母集団の平均値に近いですし、サンプルの普遍分散は、母集団の分散に近いです。
これで「問題」ができました。問題は「この10個のサンプルデータだけから、母集団の平均値を推定せよ」です。そしてもちろん正解は5です。
Rコマンダーウィンドウのメニュー下に、
データセット[UniformSamples] [編集][表示][保存]
という表示があると思います。これが、これから解析するデータです。もしデータを見たければ[表示]を押せば、データが見られます。
ここで[標準メニュー][統計量][平均][1標本t検定]を選ぶと、項目を入力するウィンドウが出てきますが、全てそのままで[OK]を押します。すると、たとえば
----------------------------
> with(UniformSamples, (t.test(obs, alternative='two.sided', mu=0.0, conf.level=.95)))
One Sample t-test
data: obs
t = 7.1259, df = 9, p-value = 0.00005509
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
3.899900 7.527671
sample estimates:
mean of x
5.713786
-----
と表示されます。細かい数値は、(サンプルデータにより)若干違うと思います。最後の「mean of x 5.713786 」は、10個のデータの平均値が5.713786 だということです。「 p-value = 0.00005509 alternative hypothesis: true mean is not equal to 0」は、「p-value は0.00005509 対立仮説:母集団の平均値が0でない」で、「もし母集団の平均値が0で現在のデータが偶然得られた(帰無仮説)のなら、その確率は0.00005509である」という意味です。これは極めて低い確率ですから「母集団の平均値は、たぶん0ではないだろう(平均値の検定)」ということが分かります。「95 percent confidence interval: 3.899900 7.527671」は、「母集団の平均値は、95%の確率で、多分3.899900~7.527671の間にあるだろう(95%区間推定)」という意味です。正解(母集団の平均値)は5ですから、まあ妥当な結果でしょう。
もう一度解析してみましょう。さっきは「もし母集団の平均値が0で現在のデータが偶然得られたのなら」という仮説で確率計算をしましたが、今度は「もし母集団の平均値が5で、現在のデータが偶然得られたなら」というう仮説で計算してみます。
ここで[標準メニュー][統計量][平均][1標本t検定]を選ぶと、項目を入力するウィンドウが出てきます。ここで「対立仮説」のところを、
◎母平均μ≠μ0 帰無仮説:μ≠μ0:μ0 =[ 5 ]
と入力し、[OK]を押します。すると、たとえば「p-value = 0.3965 alternative hypothesis: true mean is not equal to 5」と表示が変わります。
これは、「もし母集団の平均値が5で現在のデータが偶然得られたのなら、その確率は 0.3965である」という意味です。40%くらいの確率でおこることですから、まあ「普通に起こること」ですね。
なお区間推定は(母平均の検定のための仮説とは無関係ですから)、先ほどと同じで「95 percent confidence interval: 3.899900 7.527671」です。つまり区間推定だけ行いたければ、帰無仮説のところには何を入れておいても構いません。なお、「もっと確実なことを知りたい」と言う場合には「信頼水準」をたとえば0.99(99%)とか、0.999とか入力すればよいです。
かなりおおざっぱですが「正規分布でない母集団からランダムサンプリングで得られた、たった10個のデータだけからでも、この程度には、母集団の平均値、を推測できる」ことが分かるかと思います。なお、「サンプル数が多い場合、あるいは少ない場合には正規母集団と近似できる場合」つまり「母集団が正規分布をしておらず、かつサンプル数が極端に少ない場合」以外は、場合分けせずにRの「t検定」で同じ統計分析ができます。なお母集団が正規分布とかけ離れている場合には「平均値は推測できるが、母集団の代表値として平均値がふさわしいかどうかは、別問題」であることも意識しておくと良いでしょう。
では、ここまでのEZRでの操作を、動画で復習ておきましょう。一度動画を見てから、そのあともう一度じっくりと説明の文書を読みながら操作するのも良いでしょう。
t検定動画
1)平均値\(\mu\),標準偏差\(\sigma\)の母集団から、大きさ\(n\)のサンプルをランダム抽出し、その平均(サンプル平均)を確率変数\( Y \)とすると、その確率分布は、正規分布\( N(\mu,\sigma^2/n )\)になる(中心極限定理)。この性質を利用してサンプルから母平均が推定される。なおR(EZR)では、上位互換のt分布が使われる。
2)「サンプル平均を得る」という試行を多数回行えば、確率密度に比例する頻度分布が得られるため、サンプル平均の頻度分布からサンプル平均の確率密度のイメージを作ると良い(ただし計算には必要ない。)
3)「サンプル平均を得る」という試行を多数回行えば、 \( Y\) の平均値\(E(Y)\)は母平均に一致し、サンプルの不偏分散の平均\(E(\hat{s}^2)\)は、母集団の平均値\(\mu\)と母集団の標準偏差\(\sigma\)に近づく。その性質を利用し、母集団の分散が分からない場合には「不偏分散が母集団の分散に近いと近似して」扱う(この近似を行うことが大前提であり、R(EZR)は自動でそう計算しています)。
4)「母集団の平均値がμ0であり、そこから\(n\)個のデータをランダムに抽出した(それ以外何もない)」という仮説を「帰無仮説(Null hypothesis)」と呼ぶ。必要があれば(母平均の仮説の検定をしたければ)、R(EZR)での解析時、この(母平均の仮説μ0)を入力します。
5)帰無仮説の元で、得られたサンプル平均が「 μ0 くらいの範囲外」である確率をp-valueと呼ぶ。p-valueが大きければ「そのくらいずれることは、普通におこる」、p-valueが小さければ「そんなに大きくずれることは、あまりない」という意味になる(母平均の検定)。
6)「偶然起こることは無いだろう」と判断する確率の基準を「有意水準」と呼ぶ。例えば有意水準1%とは「1%未満の確率の事は、起こらないと「判断」しよう」という意味。p-value が有意水準より小さければ、「帰無仮説は棄却」される。帰無仮説の反対の命題を「対立仮設」と呼ぶ。帰無仮説の棄却は対立仮設を受け入れることになる(つまり偶然ではなく「何か(傾向とか因果関係とか)」がある)。という論理で「有意な(意味のある)」結論をひきだそうとするのが「統計的検定」の考え方。「統計的に有意でない=帰無仮説で普通に(偶然)起こること。」「統計的に有意=帰無仮説では(偶然には)起こりにくい(起こらないと判断)」という意味です。なお「有意な結果が得られた」と言うのは「その結果が正しいということでは無い」ことに注意(健康食品のCMで多用されるごまかし方法)しましょう。なお、有意水準という考え方は使い方に注意です。たとえば、有意水準1%の判断とは、確率 1.00001% は「偶然おこる」0.99999% は「偶然起こらない」と判断することであり、現実にはどちらも殆ど同じ確率のため、その違いは無意味です。本来連続的な確率値を「ある値より大きいか小さいかだけで機械的に判断することは、問題がある」との認識で、現在では「p-value」を報告することが推奨されています。
7)計算はR(EZR)で簡単に行える(計算するための公式を無闇に覚える必要はない)。
サンプルデータを与え、メニューから[1標本t検定]を選択し、必要があれば「予想する母集団の平均値を\(\mu_0\)に入力」し「区間推定をする場合の、信頼水準(確率)」を入力して、[OK]を押すだけ。すると「平均値\(\mu_0\)の母集団からランダムサンプリングで今回のサンプルデータが得られる確率」がp-valueとして得られる。p-value が「起こりえないと判断するほど小さい確率」であれば、その対立仮説「母集団の本当の平均値は入力された\(\mu_0\)ではない」という仮説が支持されます。また、母平均は、指定された信頼水準で「どの範囲にあると推定されるか(信頼区間)」が出力されます。
-- 補足 --
# なお、検定には、細かく言えば片側検定、両側検定などありますが、ここでの説明は全て「両側検定」です。実用上は殆ど「両側検定」を使いますし「十分信頼できる結果を議論する場合(p-valueが十分小さい場合)には、p-valueは片側と両側で最大でも2倍程度しか変わりません」ので、片側の話は省略します。なお確率の判断は、確率の細かい数値ではなく、おおざっぱには確率の桁数(確率が、およそ1/10か,1/100か,1/1000か,1/10000か,1/100000か...ということ )が重要ですので、2倍程度の違いは(十分信頼できる結果を議論するときには)あまり影響しません。片側について詳しく知りたい方はテキストを参照してください。なおR(EZR)で片側検定をする場合は、対立仮説のところで[母平均μ<μ0]や[母平均μ>μ0]を選択します(両側検定なら[母平均μ≠μ0です)。
# 健康や医療・保健および生物学や人文分野では「実験や調査報告の再現性が無い(他の人が同じことを追試すると異なる結果が得られる)論文が多い」ということが問題視されています。これは、特に(人間も含めた)生き物を相手にする分野では、実験や調査に様々な要因が絡み合うため「再現できる結果が得られにくい」ということも関係しますが、再現性の無い一番の原因が「有意水準5%の習慣」とも言われています(昔は数表で計算しましたし5%の数表が普及していました)。有意水準5%で「有意」と判断するなら、それは「1/20の確率で誤り」ですから、平均的に、有意水準5%で「有意な結果が得られた」と報告をしている論文20本に1本は誤りである、ということになります。ですからp-valueに基づいた正しい判断を使うか、あるいは有意水準という考えを使うなら(10%や5%は論外で)せめて0.5%以下(これなら誤りの確率1/200)にしよう、というのが「まともな研究者」の意見のようです。つまり「有意か有意でないか2つに1つという、デジタル的(間違った2分法的)判断」ではなく、アナログ的(量的)に「**%くらいの確率(p-value)で、多分**だろうと判断する」「**%くらいの確率(p-value)で、**かもしれないということが示唆された」「**%くらいの確率(p-value)で偶然起こりうることなので、ここから(偶然ではなく)ある傾向があると主張することはできない(傾向があるかもしれないし、傾向がないかもしれない=分からない)」など、「正しく」判断するように、ということです。これについては後でまた説明します。
#また、EZRのメニューは[統計解析][連続変数の解析][1標本のt検定]でもできますが、こちらは「信頼水準の日本語表示に誤りがある(信頼水準を変えても常に信頼水準95%と表示される)」ので、混乱を避ける意味で、まず「標準メニュー」の方を紹介しました。計算は正しく行われ、英語表示の方は正しく、日本語表示だけの問題ですので、実害はあまり無いのですが、これも昔の「5%有意の習慣」のためのバグと言えるかもしれません。詳しくは次回説明します。
-----
今回は「正解(母集団)が分かっている問題」で、平均値の検定・推定の練習(紹介)を行いました。
次回は、もうすこしいろいろな「正解の分かっている問題(母集団が正規分布の場合や、極端に小さいサンプル(極端にデータ数が少ない)場合や、大きなサンプル(データ数が多い)場合など」の解析を紹介します。今後は、基本的に毎回EZRを使いますので、基本的には演習室PCの利用を念頭において説明します(なお、自力でEZRを自分のPCにインストールできる方は、それを使っていただいても構いません)。いくつかの「正解の分かっている(練習のために作った)問題」の解析結果を踏まえ、最後に「実際の、正解がわからない問題(実際の実験や調査からサンプルデータのみが得られる問題)の場合」の、平均値の検定や推定の仕方と、結果の解釈や注意点などを、紹介していきます。
# なお以前紹介しましたが、EZRは、元々のR(Rコマンダー)をベースに、自治医大埼玉医療センター血液科の先生が改造して公開しているものですから、オリジナルの情報は、http://www.jichi.ac.jp/saitama-sct/SaitamaHP.files/statmed.html にあり、ここから無料でダウンロード・インストールできます。大学演習室のPCではなく、「自分のPCで使ってみたい」人は、このページから、EZRをダウンロード・インストールしてください。なお、Windows PCの場合には説明の「方法1」でインストールすると簡単です(大抵の場合にはトラブル無しで簡単にインストールできます)。ただし「インストールするフォルダー名に一部でも漢字(全角文字)が含まれていると正常に動かない(アカウント名を全角文字にしているとこういうことが起こることがあります)」とか「OneDrive上にインストールすると正常に動かない(PCのログインアカウントをマイクロソフトアカウントにしていて、ユーザ領域をOneDrive上に作っている場合に、こういうことが起こることがあります)」ということがありますので「あまり普通ではない設定をしたPC(アカウント名やフォルダー名を半角英数字のみにしていない設定をしたPC)」を使っている方は、注意してください(この説明で理解できない方は、上手く行かない場合には、とりあえず演習室のPCを使ってください)。自分のPCでEZRを使えるようになることは、この授業の範囲外(授業では演習室PCの利用を前提)としていますが、自分のPCにEZRをインストールすることは「いつでも何処でも、自分のPCを使って(EZRを利用して)統計処理ができる」ことになりますので、今後「統計解析を実際に使おう」という方にとっては、極めて重要なこと(とても強力な武器を手に入れること)になると思います。ですから、「資料を見ながらインストール試みたが、上手く行かない」という相談は、授業と関係なく、いつでも受けるつもりでいますので、そういう方はあらかじめメールなどでアポを取ったうえで、「研究室に、実際にPCを持って、相談(質問)」してください。なお、「上手く行かない」だけの情報ではアドバイスのしようがありませんから、必ずPCを持ってきて実際に「(上手く行かないとは、)どうなるのか?」を見ながら、相談にのります。
また、以前紹介しましたが、「この授業で紹介するEZRの使い方の動画」は、今回の物も含め、予習・復習で使えるように、https://www.u-kochi.ac.jp/~kazama/UOKLMS/statistics/sample.html に入れておきますので、ブックマークに登録し、適宜、以前紹介し体験していただいた「記述統計」の処理の仕方の復習とか、今回の動画も含め今後体験していただく「統計的推定」の仕方の予習とかに、参照していただければ良いと思います。
では、今日は、このへんで終わります。