今まで「２つの事象(A,Bとか)」を扱ってきましたが、もっと沢山の事象を取り扱っていきましょう。そしてまずは、「２つの事象が同時に起こることが無い」場合から整理していきます。今までは\( {\rm A}\), \( {\rm \bar A}\) と書いていた内容です。「同時に起こることが無い関係にある事象」を「排反事象」と呼びます。たとえば１つのサイコロの場合、「１が出る」「１が出ない」の２つの事象が同時に起こることがありませんから、排反事象です。また「１が出る」「２が出る」「３が出る」「４が出る」「５が出る」「６が出る」の６つの事象は、同時に２つのことは起こりませんから６つの事象は「互いに背反事象」と言います。
では、この６つの排反事象に名前を付けていきましょう。A,B... だと直ぐに名前がなくなってしまいますから、 X1, Ｘ2, ... Xn , のように、数字を添え字に使いましょう。今の場合、X1, Ｘ2, Ｘ3,Ｘ4, Ｘ5, X6 と名前を付けます。そしてそれぞれの事象をP(事象)と書くなら、\( P(X_1)\)、\( P(X_2)\)、... と書けばよいことになります。
ここで\(X\)という変数を導入します。この\(X\)の値が1なら事象X1を、\(X\)の値が2なら事象X2を表すことにします。つまり「変数の値で事象を表現する」ことを行います。なおこれが可能なのは「考えている事象が互いに背反であり、考えている事象を１列に並べることができる場合」です。その場合には、「１つの数」で「1つの事象」を表すことができます。この考え方を「確率変数」と呼びます。特に、事象の間に「（整数と同じように）順序関係や大小関係」がある場合には、後で「～以下の場合」とかの概念が意味を持ちますので、事象を整数の値で表す方法は便利です。
なお、この段階では事象を分類しただけで確率と何の関係ないのですが、（だから本来は「事象変数」とでも呼ぶべきものですが）、後で確率分布のグラフを書くときにグラフの「横軸」として使いますので、先回りしたような変な用語が使われていますので、用語は確率変数、意味は事象変数とでもいうべきもの、と理解しましょう(^^; なお「確率変数」だけでなく、後で出てくる「確率関数、確率密度関数、分布関数、累積分布関数」等も、名前と意味がぐちゃぐちゃです(^^;
ちょうど犬にタマ、猫にポチという名前を付けるような違和感がある用語が、普通に使われています(^^;
サイコロの目の問題の場合、「サイコロを振り、出た目をＸとする。おこること（事象）は、X=1,2,3,4,5,6 の６種類であり、互いに背反である」と確率変数Ｘを用いてまとめることができます。そしてそれぞれの事象に対する確率は、（事象をＸと書きますから）\( P(X), X=1,2,3,4,5,6\)、とまとめることができます。
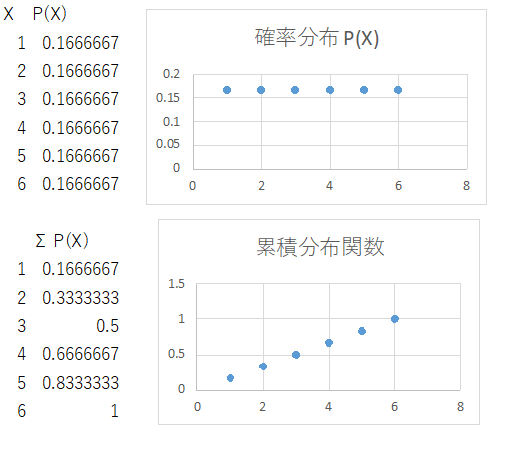
すると、そぞれの事象に対する確率は「グラフ」で表すことができます。値はすべて1/6ですから、グラフは右図のようになります。
このグラフで表されたもの、つまり関数\( P(X)\) を「確率分布あるいは確率関数」と呼びます。サイコロの例でいえば「サイコロの目がXである確率」です。 また、事象を区別する変数\(X\)を確率変数と呼びます。今の場合、変数\(X\)は、1,2,3,4,5,6という「整数値」しか取りません。サイコロの目が1.5 とか無いですよね？(^^; このように「確率変数が、整数値のような、とびとびの値」であるとき、この分布を「離散確率分布」と呼びます。離散とは連続に対する言葉で、まあ離散とは「自然数や整数のようなもの」「連続とは、実数や直線のようなもの」と捉えていただけたら、良いのではないかと思います。今風に言うなら「デジタル＝離散＝整数」「アナログ＝連続＝実数」と捉えていただいても良いです。
また、\[ F(N) = \sum_{X=1}^{N} P(X) \]を、累積分布関数（あるいは単に分布関数）と呼びます。このサイコロの例でいえば「サイコロの目がN以下の確率」を意味します。
# 犬にタマという感じの用語ですよね(^^; 多くの本で分布関数と言う用語を使っていますが、確率関数の和をとったものなら「分布関数」より「累積関数」の方が意味が通ります。しかし累積関数と言う用語を使っている本は殆どありませんので、私は累積分布関数と言うことが多いです。
サイコロの場合「１の目も、２の目も... 全部確率が同じ場合」には、確率分布は、一定となります。これを「一様な確率分布」と言います。では、一様な確率分布の時、実際に何回かサイコロを振った時にランダムに出る目の「頻度」はどのようになるのでしょうか？ ここでは実物のサイコロを振るかわりに、Rの中にあるサイコロで試した結果を紹介します（やり方はちょっと面倒なので、後程紹介します）。
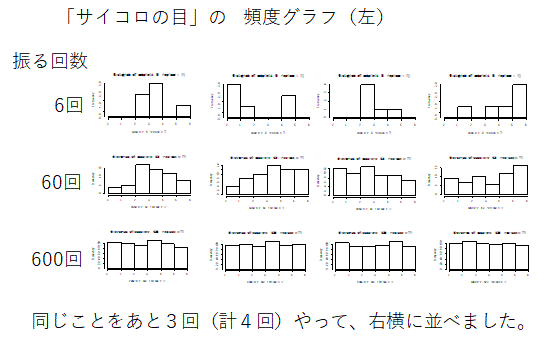右図に、その結果を示します。どれも「確率一定」の下で得られたグラフであることに注意してください。
既に「頭では（知識では）」知っていることかもしれませんが、回数が多ければ頻度分布もほぼ一定になりますが、回数が少ないと頻度分布は一定にはなりません。それが「確率一定」の性質です。そして、今の場合は「確率一定」という正解が分かっている問題のグラフです。
では逆に、ある調査とか実験とかして6つのデータが得られ、その頻度分布が「右図上、あるいは60個のデータが得られ右図中のようなグラフが得られた」場合、正解の通り、皆さんは正しく「確率は一定であり、何の傾向もない」と判断できますか？ このグラフから正しく「何の傾向もない」と判断するポイントは「回数（データ数）」です（もうちょっと正確に言うと「傾向があるとは言えない」が本当の正解です）。
テキストP.49からの部分に書いてあることが、同じことです。例えば、上右の図を見て「大きい目が出やすい傾向がある」という「妄想」を人は抱きやすいですし、「ランダム（でたらめ）は、意味ありげに見える（錯覚）」ので、注意しましょう。少なくともこの程度のデータ数の場合、傾向があるかどうはは分からない（傾向があるとは言えない）、と即座に判断できる程度のセンスを磨いておきたいものです。
タイトルにいきなり慣れない言葉があるかもしれませんが、最初は無視してください。じゃんけんやサイコロの話です。どっちでも良いですが.... まずは意表をついて、どっちでもないコイン投げの話にしましょう(^^;
どのコインでもいいので「コインを１枚」用意してください。表が出る確率は1/2とします。
---
では、コインを投げます。
表ですか？ 裏ですか？
またコインを投げましょう。表ですか裏ですか？
また.... 100回繰り返しました(^^;;
では、100回中何回表が出ましたか？
----
じゃんけんでも良いです。前に紹介した例で「チョキを出したか出さなかった」を考えます。グー・チョキ・パー全て出す確率が等しく、チョキを出す確率が1/3の場合を考えます。
---
では、じゃんけんします。
チョキですか？ チョキで無いですか？
またじゃんけんをしましょう。チョキですかチョキで無いですか？
また.... 100回繰り返しました(^^;;
では、100回中何回チョキが出ましたか？
---
これらが、これから（今回と次回）取り扱う問題です。「１回」行うと確率ｐで「ある事象が起こる（表、チョキ）」。これを何回か行い、そのうち「何回、ある事象が起こったか」を考える、と言う意味で、どちらも同じ問題です。もうちょっと整理しましょう。
今「（２つに１つの）事象A」を考える（Aが起こるか起こらないか、２つに１つ）。これを「ベルヌーイ試行」と呼びます。あ、名前は覚えなくても良いですが、本などにそう書かれることが多いですので、ベルヌーイ試行と言う言葉が出てきたら難しい言葉と思わず、「Aが起こるか起こらないか、２つに１つ」と言う問題を指していると思ってください。Aが起こるか起こらないかだけですので、Aが起こる確率を \(ｐ\) と書くことにします（もちろんAが起こらない確率は \( 1-p \) です）。
この「Aが起こるか起こらないか（ベルヌーイ試行）」を何回か繰り返します（ \( n\) 回繰り返しましょう）。そのうち何回Aが起こったのか？（ \( x \)回としておきましょう）。つまり、確率\(p\)の出来事は、何回も試行したら、どのくらい起きるのか？ もちろん一回もおこらないこともあれば、全てということもあります。確実なことは分からないです。でもどのくらい、このことがあり得そうなのか? つまり、コインの場合、確率 \(p\) で表が出るコインを、\( n \) 回振ったら、\( x \) 回表が出る確率は？ じゃんけんの場合、確率 \(p\) でチョキを出す人と、\( n \) 回じゃんけんしたら、\( x \) 回チョキが出る確率は？ という問題を考えてみましょう。
その答えは、
\[ P(確率pの事象が、n回中x回起こる) = \ _n C_x \ p^x \ (1-p)^{n-x} \]
\[ = B(x,n,p) と書く\]
となります。これを「２項分布(binomial distribution) 」と言います。
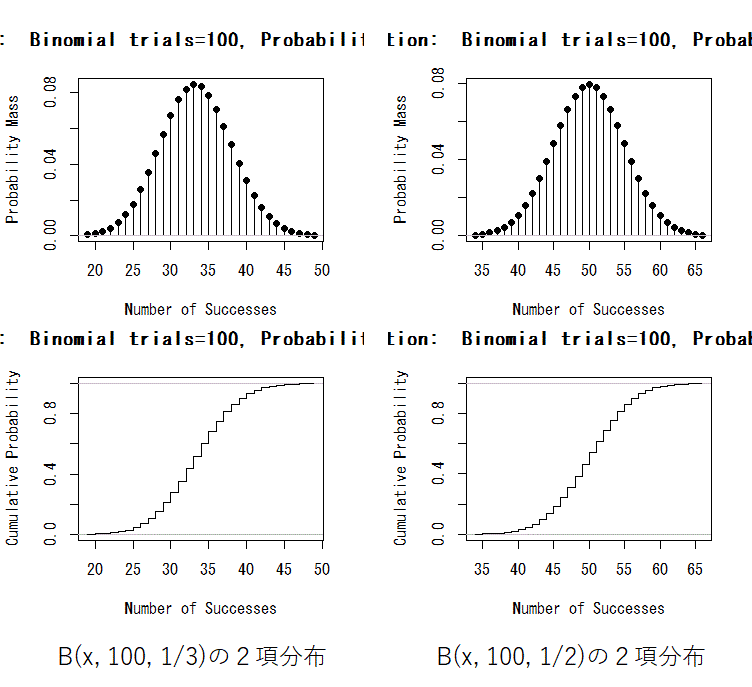図の右が「コインが１００回中ｘ回表になる確率」
左が「ジャンケン１００回中ｘ回チョキがでる確率」です。
上が確率関数、下が累積分布関数です。
コインは50回くらい表のことが多いですが、必ずしも50回ではなく、まあ40回～60回くらいが多いのかな？ と言う感じで読み取れると思います。またじゃんけんは、チョキが３３回くらいが多いですが、まあ25回から45回くらいが多いかな？ と読み取れると思います。
そのような結果から、２項分布の平均値は \( n p \) になることも、なんとなく感じ取れると思います。
なお、「１つのコインを100回振った時、何回表が出るか？」と言う問題と「100個のコインを一度に振った時、何個表が出るか」という問題は、本質的に同じになりますので、こちらの問題をかんがえることもあります。
なお、「２項分布の関数の値」は、Rならば、 dbinom(x, n, p) で得られます。またEZRでグラフを得るには、[標準メニュー] -->[分布] --> [離散分布] --> [2項分布] --> [2項分布を描く] で、「試行回数」にｎを、成功の確率にｐを、確率関数（確率分布）を書きたいのか、累積分布関数（分布関数）を書きたいのかで黒丸を付けて、[OK]で、書けます。是非ともやってみてください。
-- 余談 --
・何故「２項分布」と言うかと言えば.... この分布に現れる係数\( _{n} C_{k} \)を、２項係数と言うからです。ではなぜこの係数を２項係数と言うかは、２つの項を持つ式のべきが、
\[ (x+y)^n = \sum_{k=0}^{n} \ _n C_k \ x^k \ y^{n-k} , ここで _n C_k = \frac{ n ! }{k ! \ (n-k) ! } \]
と展開されるという定理があり（２項定理と呼ぶ）、そのときに出てくる展開係数だからです。つまり、確率の話とは全く無関係なネーミングだと思って、固有名詞として覚えてください(^^;; ただし、ｎ個の事象あるいはｎ個の因子の中から、k個選ぶという話は、確率の話でも式の展開の話でも、同じと言えば同じですが... まあ,名前の由来はあまり気にしないでください(^^;
--（怖いもの見たい方への余談... ＝怪談?(^^;）---
・「１つのコインを100回振った時、何回表が出るか？」と言う問題と「100個のコインを一度に振った時、何個表が出るか」という問題は、本質的に同じなのはなぜ？... と問われたら、実は時間と空間の対称性とかアンサンブル平均と時間平均の関係とか、エルゴード性がとか... とても難しい話が必要になるので省略します。「怖いもの見たい」方は、統計力学の本や時間空間の対称性についての物理の本を見ると良いかも(^^; なおこれは数学の問題と言うよりは時間と空間の構造、つまり物理学の問題です。
・２項係数は階乗で書くことができますが、式変形に使う以外には（値を求めるのには）実用的ではありません。現実的には、「２項係数はPCで求めるもの」と思っても良いと思います。
なお階乗計算は 1!=1, 2!=2, 3!=6, 4!=24 .... となりますが、値が大きくなるに従って「びっくりするほど大きく」なります。たとえば100! は、
100 ! = 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
です。もうちょっと大きな場合、たとえば1000 ! は、
1000 ! = 402387260077093773543702433923003985719374864210714632543799910429938512398629020592044208486969404800479988610
19719605863166687299480855890132382966994459099742450408707375991882362772718873251977950595099527612087497546249704360
14182780946464962910563938874378864873371191810458257836478499770124766328898359557354325131853239584630755574091142624
17474349347553428646576611667797396668820291207379143853719588249808126867838374559731746136085379534524221586593201928
09087829730843139284440328123155861103697680135730421616874760967587134831202547858932076716913244842623613141250878020
80002616831510273418279777047846358681701643650241536913982812648102130927612448963599287051149649754199093422215668325
72080821333186116811553615836546984046708975602900950537616475847728421889679646244945160765353408198901385442487984959
95331910172335555660213945039973628075013783761530712776192684903435262520001588853514733161170210396817592151090778801
93931781141945452572238655414610628921879602238389714760885062768629671466746975629112340824392081601537808898939645182
63243671616762179168909779911903754031274622289988005195444414282012187361745992642956581746628302955570299024324153181
61721046583203678690611726015878352075151628422554026517048330422614397428693306169089796848259012545832716822645806652
67699586526822728070757813918581788896522081643483448259932660433676601769996128318607883861502794659551311565520360939
88180612138558600301435694527224206344631797460594682573103790084024432438465657245014402821885252470935190620929023136
49327349756551395872055965422874977401141334696271542284586237738753823048386568897646192738381490014076731044664025989
94902222217659043399018860185665264850617997023561938970178600408118897299183110211712298459016419210688843871218556461
24960798722908519296819372388642614839657382291123125024186649353143970137428531926649875337218940694281434118520158014
12334482801505139969429015348307764456909907315243327828826986460278986432113908350621709500259738986355427719674282224
87575867657523442202075736305694988250879689281627538488633969099598262809561214509948717012445164612603790293091208890
86942028510640182154399457156805941872748998094254742173582401063677404595741785160829230135358081840096996372524230560
85590370062427124341690900415369010593398383577793941097002775347200000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000000000000000000000000
となります（長いので途中で改行入れましたが、全部繋げて１つの数です）。
ですから、たとえば「千個の中から３百個とりだす場合数ですら
\(_{1000} C_{300} \)＝5428250046406140648153585038929025995880600755604351798523010164122536020098000318722327614208043065399762208102049
136777969611283926864428685247418157328920246131370135991704439398156813138275163088548204192354575785444895517496303
02863689773725905288736148678480
「５千個の中から３千個とりだす場合数なら
\(_{5000} C_{3000} \)＝ 3073001093837958534311164332449228868221329099348931721694412897392573847230036365670717814145796370076634694594967
747546618177552677578420767861247446960849505600973093518295336450178188296019336901591643237281956721147475484062119
706556036984061708417095401304002783157573433873075130849947768142769762505437755441869285745101991658703036391300803
593539003688976427676326730463046167964570333162367068018231648775023096756557550835600640218705704092062510770705945
404651660558985204317317201740036859379803918484719550701561609461228078483688160018093372116295965741600333292813485
684840607296499347837267667350307187323592935011778601815163139709984445989999855949896808095167409592914481526237317
798746621082028961483990652640699091233157895696186950179771451929506493063979504028746526885399571252226024600590132
723770407481519513998089249497434145486874547259338419100232890813199057121581029295965862917280208571547945104480202
409271939856073112992341256252901290951843850728116244176383697618379286683159025199386535597348757931673057884470357
971326069595612770066113944375248886165515518192508972172165449548359962783419347260000573764013828811393518003146596
076151994048425130034716141209915905107798394762051713120826871964592306349249320117484453376728772126208511231525098
352416966658573576052954822391385452453862182473150101186342952753352384167123780730728862530330961251403614538000323
1679568297883096707543006084017128604743537323626184070400
となります。ですから、こういう計算はコンピュータに任せます(^^;
♯ なおこういう「人間なら絶対にやらない（やれない）計算」を正確に行うには、（Rではなく）Maxima（wxMaxima） というソフトを使います。これも演習
室PCに入れてあります。なお、統計の計算には正確な計算は必要ありませんので、Rでは適切な近似式を使って実用的な範囲で最終的な答えを
求めています。
まとめ
・「確率ｐでAが起こる（=確率1-pでAが起こらない ）」という「結果は２つに１つ」と言うことを行うことを、「確率pのベルヌーイ試行」という。
・上記の「確率pのベルヌーイ試行」をｎ回繰り返したとき、AがそのうちX回起こる確率B(x,n,p) を「２項分布(binomial distribution)」と呼ぶ、
・2項分布の確率関数B(x,n,p)の値は、Rではdbinom(x,n,p), 累積関数（分布関数）はpbinom(x,n,p)で得られる。
次回は、「具体的な数値」を見ながら、２項分布に従う確率計算を行い、「得られた確率値から」判断する方法（２項検定）を紹介します。
前にじゃんけんの話題で（もしチョキを出す確率が1/3なら、100回中70回チョキが出たことは、どう解釈すべきか？）という問題です。また、A・Bどちらが良いかアンケートを取って「10人中7人がAが良い」と答えたら、どう判断しますか？ 今回学んだことを元に、そのような問題を扱います。
では、今日は、このへんで終わります。