まず、前回までに学んだ「オイラーの公式」\[ e^{ix}= \cos(x) + i \sin(x) \]を思い出しておきます。この関係は、指数関数や三角関数を「多項式(テイラー展開)で定義する」ことにより、導出・証明されました。この関係式を使うと、「三角関数の加法定理は、指数関数の指数法則と本質的に同じ」「三角関数の微積分は、指数関数の微積分と本質的に同じ」になりました。
今回は、この関係式を使い「複素数」の演算規則を「図形的に理解する」ことを試みましょう。もちろんオイラーの関係式を使わない段階でも複素数を図示することができますが... オイラーの関係式を使い詳しく考察することにより、「\(i\)って何? なんで\(i^2=-1\)になるの? そんな数存在するの?」という、高校までの数学では曖昧な事柄が、中学生にでもわかるような「数直線の(平面への)拡張」であるという認識にたどり着けます。
では、順を追って、説明していきましょう。
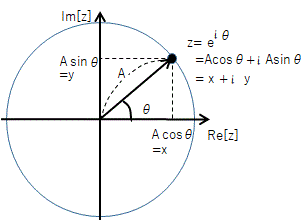
まず、オイラーの公式\[ e^{ix}= \cos(x) + i \sin(x) \]の\(x\) を\( \theta\)と、記号を変えておきましょう。理由は後で\(x\)という文字(記号)を別の意味で使いたいからです。すると、\[ e^{i\theta}= \cos(\theta) + i \sin(\theta) \]となります。右辺の三角関数の中身が\(\theta\)ですから、なんとなく\(\theta\)は角度に相当する量である、というイメージが湧きやすいと思います。ここで、両辺に、実数 \(A\) を掛けておきましょう。すると、\[A e^{i\theta}= A \cos(\theta) + i A \sin(\theta) \]という式が得られます。
ここで、 \[ A \cos(\theta)=x,A \sin(\theta)=y \] とおきましょう。逆に言うと (\(A,\theta\)でまとめると )、 \[ A= \sqrt{ x^2+y^2} , \tan(\theta)=\frac{y}{x} \] と言っても良いでしょう( 一般に \(\sin^2(\theta)+\cos^2(\theta)=1, \tan(\theta) =\sin(\theta)/\cos(\theta)\)であることを用います)。これは、「任意の \(x,y\) で表される量を \(A, \theta \):で表すことができる」という式になります。そして、 \[A e^{i\theta}= x + i y \] という式が得られます。
ここで、任意の複素数\(z\)を考えます。任意の複素数\(z\)は、2つの実数 \(x,y\) を用いて、一般に\[z=x+iy\]と書けます。\(x\)を「実部(実数部分: Real Part)」、\(y\) を、「虚部(虚数部分:Imaginary Part)」と呼びます。つまり「複素数:Complex number」と言うのは、「\(x,y\)2つの実数の組(複合:Complex)」を、1つの記号\(z\)表している、という意味です。複素数\(z\)から、実数部分を取り出すことを、\( Re[z]\) と書くことがあります。この記号を使えば、\( Re[z]=Re[x+iy]=x \)です。同じように、複素数\(z\)から、虚数部分を取り出すことを、\( Im[z]\) と書くことがあります。この記号を使えば、\( Im[z] = Im[x+iy]=y \)です。また、「虚数部分の符号を変える演算(複素共役)」も導入しておきます、\(z=x+iy \)のとき、実数部分はそのまま虚数部分の符号を変えた数を、複素数\(z\)の複素共役と呼び、\(z^* \)と書きます。具体的には、\(z^*=x-iy\) です。すると、\[z z^*= (x+i y) (x-iy) =x^2+y^2 =A^2 \]となります。
ところで、\(x,y\)2つの実数の組ですから、横軸を\(x\) 縦軸を\(y\) とする図(平面上の1点)で表すことができます。この図を「複素平面」と呼び、これがちょうど実数の場合の「数直線」の拡張になります。
では、この複素平面を使って「複素数 \( z = A e^{i \theta } \) 」を表すことを考えてみましょう。

ではここで、「複素数の掛け算」の法則を見てみましょう。2つの複素数を、\[z_1= x_1+i y_1 = A_1 e^{i \theta_1} \] \[z_2= x_2+i y_2 = A_2 e^{i \theta_2} \] とおきます。このとき、2つの複素数の積は、 \[ z_1 \cdot z_2= (x_1+i y_1) (x_2+i y_2 ) =A_1 e^{i \theta_1}A_2 e^{i \theta_2} \] となります。 真ん中の式はデカルト座標、右側の式は極座標で同じ量を書いたことになります。ところで右側の式は、指数法則を使って、さらに纏められます。 \[z_1 \cdot z_2=A_1 e^{i \theta_1}A_2 e^{i \theta_2}= A_1 A_2 e^{i(\theta_1+\theta_2)} \] 掛け算の法則を「極座標(大きさと偏角)」で見てみると、「大きさは2つの複素数の大きさの積」「偏角は2つの複素数の偏角の和」になることが分かります。ここで特に偏角のふるまいに注目するため、「大きさ1の複素数を掛ける」場合を考えてみましょう。上の式で、\(A_2=1\)の場合を考えることに相当します。すると、2つの複素数は\( A_1 e^{\theta_1},e^{\theta_2} \)で、その積は \( A_1 e^{i (\theta_1+\theta_2 )}\)になる、ということです。つまり、ある複素数に、「大きさ1の複素数 \( \theta_2 \) を掛ける」と言うことは、複素平面上で「角度 \( \theta_2 \) だけ回す」ことに相当します。
ここで、虚数単位\(i\)を掛ける、という演算を考えます。これは\(i = \cos(\pi/2) + i \sin(\pi/2)= e^{i \pi/2 } \)ですから、虚数単位\(i\)を掛けるということは、角度\(\pi/2\)つまり90°回転する、という操作に対応します。例えば 1 に\(i\)を掛ければ(実数軸上の1の点は)90°回転した虚数軸上の1(つまり\(i\))になります。この数にさらに\(i\)を掛けると、また90°回転しますから、今度は実数軸上の-1の点になります。つまり「2回掛けると-1になる」という数は、ちょうど「反対側まで回転する半分回す」ということで「90°ずれた方向(=実数軸と垂直な方向)」を向いていることが、なんとなくすっきりと見えてきます。
なお\(i\)を3回掛ければ(90°回転を3回繰り返せば)下向き(\(-i\))に、また、\(i\)を4回掛ければ(90°回転を4回繰り返せば)元に戻る(1になる)ことも、図形的に見えてきます。
このようにオイラー公式を手掛かりにして、「複素数を平面内の点で表し、必要に応じて、極座標的見方(向きと大きさ)でとらえる」と、複素数や虚数の「本質」が見えてきます。複素数とは「2つの実数\(x,y\)で表される」数。実数は1本の数直線の(1次元の)世界。複素数は「平面の(2次元の)」世界。2次元の世界で「オイラーの公式」が成り立つようにこの2次元の世界を組み立てると、それは実部(\(x\))・虚部(\(y\))いう捉え方だけでなく、複素数の大きさ(\(A\))や偏角( \( \theta \) )が定義され、極座標的に複素数を捉えることができる。そして、そのようなとらえ方をすると、大きさ1の複素数(例えば\(i\)とか-1とか )を掛ける演算は「回転」として捉えることができる。そのようなとらえ方をすれば「虚数\(i\)」は、2回回すと反対向き(=マイナス)つまり、実数軸とは垂直なもう1つの軸を考えることだと、なんとなく見えてくると思います。
そのような意味で「虚数」は「虚」の数なんかではなく、「高い次元(2次元的)」で数を捉えたものと言う認識に到達できるのではないかと思います。
では、今日はこのへんまでにして、次回は今まで学んだことを振り返ってみましょう。