様々な情報を調べる時「全てのデータ」を調べることが困難な場合があります。その時は「いくつかのデータを選び出して集め(抽出)」、「集められたデータに基づいて、全体について推測する」ということがよく行われます。「全てのデータ」のことを母集団(population)、選び出して集めた(抽出された)データの組を標本(サンプル:sample)と呼び、標本にすくまれるデータの数を、標本の大きさ(サンプルサイズ、サンプルの大きさ)と言います。
# 元々、国勢調査などの仕方としてsampling の理論は始まりましたので、英語では全体を「population(人口、全住民の意味)」、その中から抽出されたデータの組を「sample」と呼び始めました。人口以外のデータを扱う時にpopulationという単語は多少違和感がありますが、それでも統計学分野では全体のことを「population」と呼びます。日本語訳は大元の集団という意味で「母集団」という用語(訳語)が使われますが、この用語は例外的に「日本語の方が意味が掴める」と思います。sampleは「標本」と訳されていますが、まあ現代なら日本語で「サンプル」でも良いですね。
母集団からサンプルを取る場合、いろいろな方法があり得ますが、最も理論的な解析が進み応用範囲が広いのは「出鱈目に(全て等確率で)データを抽出する」という方法です。また、抽出には「同じデータを2回選ばない(取ったデータは戻さない):非復元抽出」と「同じデータを2回以上選ぶこともありうる(取ったデータを元に戻す):復元抽出」があります。復元抽出はデータを戻しますので毎回の抽出の確率は一定ですが、非復元抽出の場合には、かこにどのデータを取ったかにより、2回目以降の確率は変化していきます。ですから「復元抽出」の方が解析は簡単です。なお、母集団が抽出するサンプルの数に比べて十分に大きい場合には、取ったデータを元に戻しても、偶然同じデータをまた抽出する確率は小さくなりますから、それが無視しうる程度であれば、本当は非復元抽出でも「復元抽出」と近似することが出来ます。以下そのような場合を扱いますので「出鱈目に復元抽出すること」を、以下単に「ランダムサンプリング」と呼ぶことにし、特に非復元抽出であることを考慮する必要があるときは(非復元抽出であり、かつ、母集団の大きさがそれほど大きく無く復元抽出と近似出来ない時は)、そのように特記することにします。
そこで以下「ランダムサンプリング」であるという仮定に基づき、解析を進めます。母集団の分布から、その数に応じた確率で「出鱈目に(ランダムに)」サンプルを抽出すると、そのサンプルの性質は、母集団の分布と関係を持ちます。母集団の性質とサンプルの性質の関係を予め「確率計算により」求めておけば、それを用いて、サンプルから母集団の性質を推測することが、ある程度可能になります。
そこでまず、「母集団の性質」と「サンプルの性質」の「関係」から、見ていきましょう。
まずイメージを掴むために、簡単な場合(サンプルサイズが極端に小さい場合)から考えていきましょう。サンプルサイズ0はあり得ないですから、最小の1個の場合から順に具体的に「サンプルの性質」を見ていきましょう。なお「サンプルサイズ」はサンプルの大きさ\(n\)、あるいは大きさ\(n\)のサンプル、とも言います。いくつのデータのサンプルをとるのか、そのサンプルを取るという作業を何回行うのかを、サンプル数と言います。2種類の数が出てきますので、どちらの意味なのか、文脈などから正確に読み取らないと混乱します。それを正確に区別するには、大きさ\(n\)のサンプルを\(N\)回とる、などと言います。
母集団から「サンプルサイズ1のサンプル(1つのデータ)を抽出」する場合。これは単に母集団から1個のデータ\( x_1\)を得ることを同じですから、(例えばサイコロやコイン投げの場合の)「1回の試行」と同じです。1つずつが「母集団の分布による確率」で得られるだけですから、例えば母集団が一山であれば、山付近のデータが得られることが多いでしょうし、(サイコロの目のような)一様分布であれば、範囲内のどのデータが得られる確率も同じです。
その値が得られる確率は、「母集団の確率分布(あるいは確率密度分布)」になりますから、これを何度も繰り返せば、ヒストグラムは母集団の確率分布に近づいていきます(しかしかなりの回数繰り返さないと「揺らぎ」が大きく、元の分布(母集団の分布)と似た形にならないこともあります)。
母集団から「サンプルサイズ2のサンプル(2つのデータ)を抽出」する場合は、(1回の試行で)値が2つ( \( x_1,x_2\) )得られます。この値は近いこともあれば、離れていることもあるでしょう。1つずつの値がとる確率は、単に母集団から1個のデータを得ることを同じです。 ここで「2つの値の和(\( x_1+x_2\))」を考えてみます。
2つのデータの値が共に大きな数なら、和は大きな数になります。2つの値が共に小さな値なら、和は小さな値になります。1つが大きく1つが小さい値なら、和は中間くらいの値になります。もし仮に「大きい・小さい」をベルヌーイ事象のように捉えれば、それを2回繰り返し和を取るのと同じですから、n=2の二項分布になります(和が小さい確率1/4,和が大きい確率1/4、和が中間である確率1/2)。今は、とりうる値が「大きいか小さいか、2つに1つ」ではないですが、連続的な場合でも、似たことが起こります。ランダムウォークで2歩あるいた時の移動距離、の問題と同じです。
では次に、和を2で割りましょう( \( \frac{x_1+x_2}{2} \) )。分布のグラフとしては、和を2で割っただけですから、横軸の目盛りを付け替えれば、和のグラフと形は同じです。また、2つの値の和2で割れば、これは2つの値の平均と同じですから「サンプル内の(2つの値の)平均」を考えていることになります。これを「サンプル平均(標本平均\(\bar{x}\))」と呼ぶことにします。また、2つの値は離れているかもしれませんので、「2つの値が、サンプル平均からどのくらい離れているか」の指標として、標準偏差を用いましょう。\( s = \sqrt{ \frac{1}{2}\{ (x_1-\bar{x} ) ^2+(x_2-\bar{x} )^2 \} } \) これを「標本標準偏差」と呼びます(\(s^2\)を標本分散と呼びます)。
なお、(先ほど飛ばしましたが)サンプルサイズ1の場合には、「標本平均\( \bar{x} \)」は、データが1つしかありませんので「データの値そのものが標本平均\( \bar{x} \)」であり、またデータが1つしかないので「標本標準偏差や標本分散は0」になります。
では、母集団がいくつかの分布関数に従う場合について、そこからサンプルサイズ1、サンプルサイズ2の時の「標本平均\( \bar{x} \)の分布」を具体的に見てみましょう。つまり「サンプルサイズ1」の試行(サンプリング)を多数回繰り返した時の標本平均(=その値)の頻度分布(ヒストグラム)を見たり、「サンプルサイズ2」の試行(サンプリング)を多数回繰り返した時の標本平均(2つの値の平均値)の頻度分布(ヒストグラム)を見たりしてみましょう。

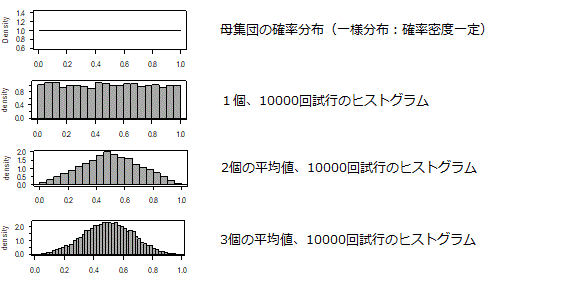
図の一番上は「母集団の分布」です。例として確率変数0~1で確率密度一定の「一様分布」の場合を示します。この母集団から「1つ」データを取ると、どの値を取る確率も同じですから(サイコロみたいなもの)、その試行を多数回(今は1万回)繰り返せば、頻度分布(ヒストグラム)は、ほぼ一定になります。それが上から2番目のグラフです。次に「2つ」データを取り「2つのデータの平均値」を求めます。その試行を多数回(今は1万回)繰り返すと、「毎回の(2つのデータの)平均値」の分布は、上から2番目のようになります。同じように「3つ」データを取り「3つのデータの平均値」を求めます。その試行を多数回(今は1万回)繰り返すと、「毎回の(3つのデータの)平均値」の分布は、上から3番目のようになります。
つまり、「サンプルの平均値」を取るという試行を多数回繰り返すと、サンプルサイズ(\(n\))が大きければ、その分布は「正規分布のグラフ」に近づいていきます。確率は、多数回試行した時におきる割合に等しいですから)「サンプルサイズ\(n\)が大きければ、サンプルの平均値の分布は、正規分布になる」ということが分かります。これを「Central Limiting Theorem(中心極限定理)」と言います。意味は統計学における「中心的な(最も重要な)」「極限に関する定理」という感じの意味です。もう少し正確に言うと「サンプルサイズ\(n\)を無限大にする極限では、平均値の分布は正規分布になる」という定理です。

今は「一様分布」から始めましたが、母集団の分布は「何でもよい」のです。母集団がどんな分布であっても「n個のサンプルの平均」の分布は、\(n\)が大きければ必ず正規分布になります。例として母集団の分布が指数関数的な場合について、示します。一番上が母艦数の確率分布、その下が1つデータを取った時の値の分布です。ここでは先ほどと同じ1万回試行を行い、頻度分布をヒストグラムで表しました。1この場合は、回数が多いですので殆ど確率分布と同じ形です。その下が2個の平均値の分布です。平均値が0付近と言うことは、2つの値とも0付近の値が選ばれなければならないので、低い確率になってきます。その下は、10個の平均値の分布です。かなり正規分布の形に近づいていることが読み取れると思います。
# 数年前、授業でこの定理を紹介した時、学生さんが「なんか、『中心極限定理』って、かめはめ波みたいでかっこいい(笑)」と言いました。詳しい意味を説明する前にです。なかなかセンスのある学生さんと思いました。まさにそういう意味です。統計学における「必殺技」という意味の名前ですから。そのくらい強力な定理です。
母集団(平均値\(\mu\), 標準偏差\(\sigma \))から、「無作為(ランダム)に\( n \)個のデータ(=サンプル:\(x_i:i=1~n\) )を抽出し、この\(n\) 個のデータ平均値(\(\bar{x}\))を\(Y\)と置く。」という試行を考える(1回の試行で\(Y\)の値が1つ決まる)。この試行を多数回行い\(Y\)の値が得られる頻度分布を調べれば、「確率変数(=\(n\)個平均値)\(Y\)が得られる確率分布」が得られる。サンプルサイズ\(n\)が十分大きなとき(\( n \rightarrow \infty \)の極限において)\(Y\)の確率分布は、 \( N(\mu,\sigma^2/n) \) つまり、平均値\(\mu\),標準偏差\( \frac{\sigma}{\sqrt{n}} \)の正規分布になる。
「サンプルの平均値\(Y\)」が確率変数であることに注意。コイン投げの場合と対比すると、
・コイン投げの場合(2項分布: 確率分布=確率密度)
確率\(p\)で表が出る\(n\)枚のコインを投げて\(x\)枚表が出る(確率\(P(x)\))
確率分布\(P(x)\):2項分布 \(B(x,n,p)\)
・母集団から\(n\)個のデータを(ランダムに)抽出し、平均値\(Y\)(くらい)を得る(確率\(dP(Y)=f(Y) dY\) )
確率密度分布:正規分布 \( N(\mu,\sigma^2/n) \)
という対応になります。中心極限定理を使用する場合には「サンプルの平均値\(Y\)を確率変数」として分布を考えていることに注意すると、イメージがつかみやすいと思います。
母集団から、十分大きな(データの個数\(n\)が十分に大きい)サンプルを抽出した場合の、「母集団の性質」と「サンプルの平均\(Y\)の分布の性質」を整理していきます。ここでは、母集団の平均値を\(\mu\), 母集団の標準偏差\(\sigma \))とおきます。これは「母集団の平均値に意味があるかどうか」とは全く無関係ですので注意してください。意味があろうとなかろうと「平均値」は(総和/個数)で定義されます。標準偏差についても同じです。
母集団から、大きさ\(n\)のサンプルを取りサンプル平均\(Y\)を求めます。これを多数回繰り返せば、\(Y\)が得られる確率分布が得られますが、それは正規分布 \( N(\mu,\sigma^2/n) \) になる、というのが中心極限定理です。
つまり、\(Y\)の分布の平均値(期待値)は、母集団の平均値(期待値)\(\mu\)に等しいことが分かります。
これは「多数回Yを求めて、その平均を取れば、母集団の平均値\(\mu\)と等しくなる」ことを意味します。
もちろん1回\(Y\)を取るだけなら、それは「\(Y\)の分布の平均値からずれる」こともあります。では「平均的にそのくらいずれる」のでしょうか? それが標準偏差です。\(Y\)の分布の標準偏差は\( \frac{\sigma}{\sqrt{n}}\)なので、 平均的にこのくらいはずれることが普通です。またそこから大きく外れるは確率は、比較的小さくなります。なお、標準偏差の大きさがサンプルの大きさ\(n\)の平方根に反比例しています。つまりサンプル数が100倍になると標準偏差は1/10になり、「\(Y\)の値が平均値から大きく外れることは少なく」なります。
「前のページのグラフ」を見ても、サンプル数が大きくなるに従い、分布の形が正規分布に近づくことに加え、「分布がシャープに(平均値の近くに)」変化しています。
この性質を利用し「十分大きな(\(n\)が大きな)サンプルの平均値は\(Y\)」は、「\(Y\)の分布の平均値(期待値)=母集団の平均値(期待値)」に十分近くなり、そこから外れる確率は小さくなるため、「1回のサンプリングでも、そのような\(Y\)の値が得られることが、普通なのか、ありえないほど小さい確率なのか」を求めることができます。
その確率の値に基づき、「サンプルから、母集団の平均値」を推定することができます。
任意の母集団に対して、「サンプルサイズ\(n\)が十分に大きければ」、平均の分布は正規分布になります(中心極限定理)が、母集団を限れば、サンプルサイズが小さい場合にも平均値の分布を求めることができる場合があります。特に「母集団が正規分布をしている(と近似できる場合)」には、「一般に、ランダムに抽出した\(n\)個のデータの平均値=サンプルの平均値、の分布」は厳密に求めらる(t分布と呼ぶ)ことを、当時ギネスビール社に勤めていたウィリアム・ゴゼット(ペンネーム:スチューデント)が求め、数学者のロナルド・フィッシャーとの意見交換の際、様々な関数を区別するためにたまたまゴゼットがこの関数を「t」と書き、それに敬意を表して、フィッシャーが「スチューデントのt分布」と呼び始め、現在でも「t分布」と呼ばれています(つまり、「tと言う名前」には意味がありません)。なお、t分布は、サンプル数\(n\)が大きいときには正規分布に近づきます。
そのため、「昔は」、場合わけして、サンプルの平均値の分布として、サンプルサイズが大きいときには「正規分布の表」を使い、サンプルサイズが小さいけど正規母集団であると近似できる場合には「t分布の表」を使うという解析が行われていました(t分布の表は、サンプルサイズ毎にありますので、手計算では多少複雑になります)。表を使って計算する場合の説明が書かれている本などだと、今でも場合わけの仕方についての説明があります。
しかしコンピュータを使う現在では、全て「t分布」で統一して計算することが普通です。これで「サンプルサイズが小さい正規母集団の場合」だけでなく「サンプルサイズが大きい時には、自動的に正規分布に移行していく」ので、実用上「正規分布であることを指定する必要が無い(場合分けする必要が無い)」ためです。ですから「t分布による解析(t検定)は、中心極限定理に基づいた(正規分布を使う)解析の、上位互換バージョン」と思っていただければよいと思います。次回、この定理に基づき、「実際に、サンプルから母集団の平均を推定する」ことを行います。R(EZR)では、この解析を「t検定(t.test)」と呼びます。
ここから先は「ちゃんと理解しようとすると、ちょっとややこしい計算が必要」になるので、この授業の範囲としては「大体のイメージ」だけ掴んでいただければよいと思っています。
母集団からサンプルデータを1つ取った時には、もちろん値が1つだけですから「分散」も「標準偏差」もありません(0です)。2つ以上のデータがあって、初めて「分散」が意味を持ちます、これを標本分散(\(s^2\))と呼びます。サンプルサイズ\(n=1\)なら\(s^2=0\)、サンプルサイズ\( n \geq 2 \)で初めて0でない標本分散になります。ところで、サンプルサイズnが十分に大きい場合(たとえば母集団のデータ全部を取った場合)には、標本分散を求めることは母集団の分散を求めることとほとんど同じですから、その場合標本分散(\( s^2\))を多数回求めた平均\(E(s^2)\)は、母集団の分散\(\sigma^2\)と一致します(ここで\( E(□) \)は多数回試行した時の平均を表す記号)。この関係は、 \[ E(s^2)=\frac{n-1}{n}\sigma^2 \] となることが示されます(テキストA.6 p166に証明あり。ちなみに\(n=1\)なら\(E(s^2)=0\)で、\( n= \infty \)なら\(E(s^2)=\sigma^2 \))。つまり、母集団の分散は、 \[ \sigma^2 =\frac{n}{n-1} E(s^2) = E( \frac{n}{n-1} s^2 ) \] ところで、 \[ s^2=\sum_{k=1}^n{\frac{ (x_k-\bar{x})^2 }{n}} \] なので、 \[ \hat{s}^2=\sum_{k=1}^n{\frac{ (x_k-\bar{x})^2 }{n-1}} = \frac{n}{n-1}s^2\] という量を導入すると、母集団の分散は、 \[ \sigma^2 =\frac{n}{n-1} E(s^2) = E( \hat{s}^2 ) \] と表すことができます。この量は\( n \geq 2 \)で初めて意味ある数値になります(\(n=1\)の時は0/0で不定)。\( \hat{s}^2 \)は、「多数回求めて平均を取れば、母集団の分散になる量」ですから、まあ、1回でも母集団の分散の(それなりの)推定値と解釈することができます。これを不偏分散と呼びます。
では母集団から「\(n\)個のデータ」を取った場合、(平均値Yの分布は正規分布になりましたが)分散はどのような分布になるのでしょうか? これは平均値Yの時の中心極限定理みたいに一般的な答えにはならず「分散の分布は、母集団の分布による」という結果になります。なお、母集団が正規分布(と近似できる)の場合(正規母集団の場合)には、サンプル分散の分布は\( \chi^2 \)分布(かいじじょうぶんぷ)になるという結果が得られています。データの「広がり具合」に対する分析などで、後で使いますので、その時にまた、\( \chi^2 \)分布について説明します。今回は予告編的に読んでいただけばよいと思っています。
長くなりましたので、今回の話を、一応まとめておきましょう。
・大元の(注目している)集団を「母集団」と呼ぶ。知りたいのは「母集団」がどのような性質を持つか?(母集団の平均値(母平均\( \mu \))や母集団の分散(母分散\(\sigma^2\))や、母集団の標準偏差(母標準偏差\(\sigma\))など)
・母集団から「いくつかのデータを抽出したもの」を「標本」あるいはサンプルと呼ぶ。サンプルの撮り方は色々あり得るが、以下「出鱈目な復元抽出(以下ランダムサンプリング)」の場合に、「母集団」と「サンプル」の関係をつける。母集団から\(n\)個のデータを取り出したものを「大きさ\(n\)の標本(サンプル)」と呼ぶ。なお、ここでは大きさ\(n\)をサンプルサイズとも表現している。。
・「大きさ\(n\)のサンプル」の平均値や分散、標準偏差を「標本平均、標本分散、標本標準偏差」と呼ぶ。
・「大きさ\(n\)のサンプルを取り、その平均値を求める」ことを1回の試行ととらえ、「標本平均が、ある値\(Y\)になる確率」を考える。標本平均\(Y\)を確率変数とした確率分布を考える、という意味。標本平均\(Y\)の確率密度分布は、\(n=1\)なら(母集団からそのまま1つデータを取っただけなので)母集団の分布と同じであるが、\(n\)が十分大きい時には母集団の分布によらず徐々に正規分布に近づき、\( n \rightarrow \infty \)の極限では母集団の分布によらず、全て \( N(\mu,\sigma^2/n) \) の正規分布になる(中心極限定理)。
・サンプル平均の分布は、特に、母集団が正規分布(正規母集団)の時は、\(n\)が小さい時でも正確に求めることが可能で、ありこれを「(スチューデントの)t分布」と呼ぶ。t分布はサンプルサイズが大きいときには自動的に正規分布に近くため「正規母集団の場合には\(n\)が小さくても成り立ち、それ以外の分布の母集団のときには、\(n\)が大きい時に近似的に成り立つ」サンプル平均の分布として(正規分布の上位互換として)、用いることができる。コンピュータを使う場合には(別のプログラムを作る無駄を省くため)「t分布」を使う解析(t検定)を行う。
・標本分散(\( s^2\))に意味があるのはサンプルサイズ\(n\)が2以上の場合である(データ1つなら分散は0)。標本分散(\( s^2\))と母分散(\( \sigma^2\))の間には関係があり、サンプルサイズ\(n\)が無限大の極限では(母集団のデータ全部を取ることを意味するから)両者は一致するはずである。不偏分散を \( \hat{s}^2=\sum_{k=1}^n{\frac{ (x_k-\bar{x})^2 }{n-1}} = \frac{n}{n-1}s^2\)と定義する。「サンプルを取り不偏分散を求める」という試行を多数回行いその平均値を取ると、試行回数が多ければ母分散に近づく。このため、不偏分散が「サンプルからとりあえず推定される母分散」的な意味になる(標本分散は、直接は母分散の推定値にはならない)。なお標本分散の「分布」は\( \chi^2 \)分布に従い、「データの広がり」に基づく解析をする場合には、この分布に基づく解析「\( \chi^2 \)検定」を行う。
・おまけ:実際の解析においては、以上のことは「ランダムサンプリングという仮定(条件)が成り立つ場合にのみ」成立することを、強く意識しておくことが重要になります。また、実際の調査などでは、本当のランダムサンプリングは、かなり困難なことが多いですし、サンプルの取り方が違えば、ここで紹介した関係が成り立たない場合があります。悪意を持って意図的なサンプリングを行えば「どのような統計的結果でも出す」ことが出来ます。行政や企業などでは「望む結果を出したい」という目的で統計調査を行うことがありますので、その仕事をする人は「望む結果が出るような意図的なサンプリングを、意図的と気がつかれないように嘘をついたり誤魔化したりして行い」そのことを隠して結果のみ報告する、ということを(仕事として)よく行います。例は... 新聞などの報道を見れば、山ほど見つかります。「世の中には3つの嘘がある。嘘、大嘘、そして統計」。統計学を装った「嘘」は大抵の場合「サンプリング」の場面で仕込みます。逆に言えばそこを注意すれば殆どの統計的「嘘」は見破れます。嘘をつくことが仕事ではなく、真実を明らかにすることが仕事の人(=学者・研究者等)は、できるだけ嘘のない客観的データ(サンプル)を取ろうとしますが、これが「不可能に近いくらい難しい」こともよくあり、その場合には「近似的にランダムサンプリングとみなせる方法」を、研究対象に応じ、いろいろ編み出し、一応それで代用しています。そういう意味で「ランダムサンプリング」と言うのは簡単だけど、実際にはとても難しい「目指すべき目標(理想)」とでも言うような扱いになることもあります。これについては、(現実のデータ解析では最も重要なことになるので)また後で振り返ることにします。
--- 以下余談 ---
今回の内容、テキストの「該当する部分」を、読んでみてください。記号が若干違うところがありますので、ピンポイント的につまみ読みだと誤解する場所があるかもしれませんが、該当部分の節や章の最初から読めば、テキストの記号も誤解なく理解できるはずと思います。また証明を知りたい場合にも、簡単なものはテキストの付録にありますので(多分高校数学程度の内容)、興味のある方はみておいてください。なお、授業にもテキストにも無い式の「証明」も、Webなどで調べればほぼ全て見つけられると思いますが、授業でもテキストでも紹介していないものは、高度な数学を使う必要がありますので、相当本気で数学を勉強してから再度挑戦してみるか、あるいは証明を諦め「そういうもんか(^^;」という程度の理解でとりあえず満足しておくことを勧めます(^^;
次回は、EZRで「t検定(t.test)」を用いて、「サンプルから、母集団の平均値を推定する」ことを行います。
では、今日は、このへんで終わります。